题目内容
【题目】如图,PA,PB是⊙O的切线,A,B为切点,点C在PB上,OC∥AP,CD⊥AP于D
(1)求证:OC=AD;
(2)若∠P=50°,⊙O的半径为4,求四边形AOCD的周长(精确到0.1)
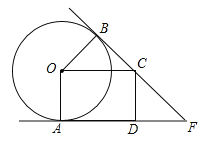
【答案】(1)证明见解析;(2)18.4.
【解析】
试题分析:(1)只要证明四边形OADC是矩形即可.
(2)在RT△OBC中,根据sin∠BCO=![]() ,求出OC即可解决问题.
,求出OC即可解决问题.
试题解析:(1)证明:∵PA切⊙O于点A,∴OA⊥PA,即∠OAD=90°,∵OC∥AP,∴∠COA=180°﹣∠OAD=180°﹣90°=90°,∵CD∥PA,∴∠CDA=∠OAD=∠COA=90°,∴四边形AOCD是矩形,∴OC=AD.
(2)解:∵PB切⊙O于等B,∴∠OBP=90°,∵OC∥AP,∴∠BCO=∠P=50°,在RT△OBC中,sin∠BCO=![]() ,OB=4,∴OC=
,OB=4,∴OC=![]() ≈5.22,∴矩形OADC的周长为2(OA+OC)=2×(4+5.22)=18.4.
≈5.22,∴矩形OADC的周长为2(OA+OC)=2×(4+5.22)=18.4.

练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目