Question

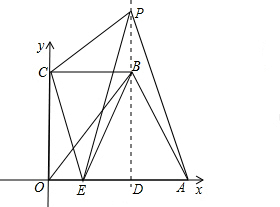
如图①，将直角梯形OABC放在平面直角坐标系中，已知OA=5，OC=4，BC∥OA，BC=3，点E在OA上，且OE=1，连接OB、BE．
（1）求证：∠OBC=∠ABE；
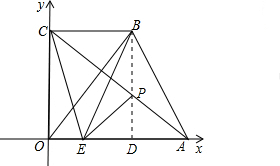
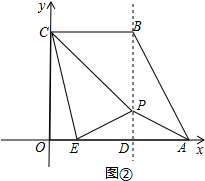
（2）如图②，过点B作BD⊥x轴于D，点P在直线BD上运动，连接PC、PE、PA和CE．
①当△PCE的周长最短时，求点P的坐标；
②如果点P在x轴上方，且满足S_△CEP：S_△ABP=2：1，求DP的长．

Answer 1

分析：（1）先由已知条件及勾股定理求出AE=4，AB=2

5

，得到

AB

AE

=

OA

AB

，又∠OAB=∠BAE，根据两边对应成比例且夹角相等的两三角形相似证明△OAB∽△BAE，得出∠AOB=∠ABE，再由两直线平行，内错角相等得出∠OBC=∠AOB，从而证明∠OBC=∠ABE；
（2）①由于CE为定长，所以当PC+PE最短时，△PCE的周长最短，而E与A关于BD对称，故连接AC，交BD于P，即当点C、P、A三点共线时，△PCE的周长最短．由PD∥OC，得出

AD

AO

=

PD

OC

，求出PD的值，从而得到点P的坐标；
②由于点P在x轴上方，BD=4，所以分两种情况：0＜PD≤4与PD＞4．设PD=t，先用含t的代数式分别表示S_△CEP与S_△ABP，再根据S_△CEP：S_△ABP=2：1，即可求出DP的长．

解答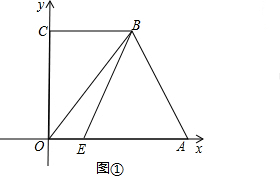：解：（1）∵OC=4，BC=3，∠OCB=90°，
∴OB=5．
∵OA=5，OE=1，
∴AE=4，AB=

42+(5-3)2

=2

5

，
∴

AB

AE

=

OA

AB

，
又∵∠OAB=∠BAE，
∴△OAB∽△BAE，
∴∠AOB=∠ABE．
∵BC∥OA，
∴∠OBC=∠AOB，
∴∠OBC=∠ABE；

（2）①∵BD⊥x轴，ED=AD=2，
∴E与A关于BD对称，
∴当点C、P、A三点共线时，△PCE的周长最短．
∵PD∥OC，
∴

AD

AO

=

PD

OC

，即

2

5

=

PD

4

，
∴PD=

8

5

，
∴点P的坐标为（3，

8

5

）；
②设PD=t．
当0＜PD≤4时，
∵S_△CEP=S_梯形OCPD-S_△OCE-S_△DEP=

1

2

（t+4）×3-

1

2

×4×1-

1

2

×2t=

1

2

t+4，
S_△ABP=

1

2

×2（4-t）=4-t，
∵S_△CEP：S_△ABP=2：1，
∴（

1

2

t+4）：（4-t）=2：1，
∴t=DP=

8

5

；
当PD＞4时，
∵S_△CEP=S_梯形OCPD-S_△OCE-S_△DEP=

1

2

（t+4）×3-

1

2

×4×1-

1

2

×2t=

1

2

t+4，
S_△ABP=

1

2

×2（t-4）=t-4，
∵S_△CEP：S_△ABP=2：1，
∴（

1

2

t+4）：（t-4）=2：1，
∴t=DP=8．
故所求DP的长

8

5

或8．

点评：本题是相似形的综合题，涉及到勾股定理，平行线的性质，轴对称的性质，三角形的面积，相似三角形的判定与性质，有一定难度．（2）中第二小问进行分类讨论是解题的关键．