题目内容
下列说法中,正确的是( )A.在Rt△ABC中,若tanA=
 ,则a=4,b=3
,则a=4,b=3B.若三角形的三边之比为1:
 :2,则三角形是直角三角形
:2,则三角形是直角三角形C.对于锐角α,必有sinα<cosα
D.在Rt△ABC中,∠C=90°,则sin2A+cos2B=1
【答案】分析:根据三角函数的定义,勾股定理,锐角三角函数的增减性,同角三角函数的关系对各选项分析判断后利用排除法求解即可.
解答:解:A、Rt△ABC中,若tanA= ,说明a与b的比值是
,说明a与b的比值是 ,不是a=4,b=3,故本选项错误;
,不是a=4,b=3,故本选项错误;
B、根据题意,设三边为k,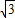 k,2k,则(2k)2=k2+(
k,2k,则(2k)2=k2+(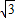 k)2=4k2,根据勾股定理,三角形是直角三角形,故本选项正确;
k)2=4k2,根据勾股定理,三角形是直角三角形,故本选项正确;
C、对于锐角α,sinα与cosα大小不能确定,故本选项错误;
D、在Rt△ABC中,∠C=90°,则sin2A+cos2A=1,故本选项错误.
故选B.
点评:本题考查了解直角三角形,是基础题,需要熟练掌握并灵活运用.
解答:解:A、Rt△ABC中,若tanA=
 ,说明a与b的比值是
,说明a与b的比值是 ,不是a=4,b=3,故本选项错误;
,不是a=4,b=3,故本选项错误;B、根据题意,设三边为k,
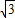 k,2k,则(2k)2=k2+(
k,2k,则(2k)2=k2+(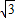 k)2=4k2,根据勾股定理,三角形是直角三角形,故本选项正确;
k)2=4k2,根据勾股定理,三角形是直角三角形,故本选项正确;C、对于锐角α,sinα与cosα大小不能确定,故本选项错误;
D、在Rt△ABC中,∠C=90°,则sin2A+cos2A=1,故本选项错误.
故选B.
点评:本题考查了解直角三角形,是基础题,需要熟练掌握并灵活运用.

练习册系列答案
相关题目