题目内容
 (2013•历下区二模)如图,点A(x1,y1)、B(x2,y2)都在双曲线y=
(2013•历下区二模)如图,点A(x1,y1)、B(x2,y2)都在双曲线y=| k |
| x |
分析:根据S矩形AEOC=S矩形OFBD=
(S五边形AEODB-S△AGB-S四边形FOCG)+S四边形FOCG,先求得S矩形AEOC和S矩形OFBD的值,利用k=AE•AC=FB•BD来求k的值.
| 1 |
| 2 |
解答:解:∵x2-x1=4,y1-y2=2
∴BG=4,AG=2
∴S△AGB=4
∵S矩形AEOC=S矩形OFBD,四边形FOCG的面积为2
∴S矩形AEOC=S矩形OFBD=
(S五边形AEODB-S△AGB-S四边形FOCG)+S四边形FOCG=
(14-4-2)+2=6
即k=AE•AC=6.
故选C.
∴BG=4,AG=2
∴S△AGB=4
∵S矩形AEOC=S矩形OFBD,四边形FOCG的面积为2
∴S矩形AEOC=S矩形OFBD=
| 1 |
| 2 |
| 1 |
| 2 |
即k=AE•AC=6.
故选C.
点评:此题综合考查了反比例函数系数k的几何意义,此题难度稍大,综合性比较强,注意反比例函数上的点向x轴y轴引垂线形成的矩形面积等于反比例函数的k值.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
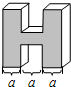 (2013•历下区二模)如图所示的几何体的俯视图是( )
(2013•历下区二模)如图所示的几何体的俯视图是( )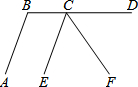 (2013•历下区二模)如图,已知CE∥AB,D为BC延长线上一点,CF平分∠DCE,∠ABD=110°.则∠ECF的度数为( )
(2013•历下区二模)如图,已知CE∥AB,D为BC延长线上一点,CF平分∠DCE,∠ABD=110°.则∠ECF的度数为( )