题目内容
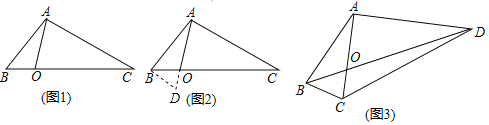
【题目】对于线段外一点和这条线段两个端点连线所构成的角叫做这个点关于这条线段的视角．如图1，对于线段AB及线段AB外一点C，我们称∠ACB为点C关于线段AB的视角．
如图2，点Q在直线l上运动，当点Q关于线段AB的视角最大时，则称这个最大的“视角”为直线l关于线段AB的“视角”．
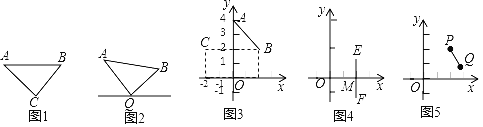
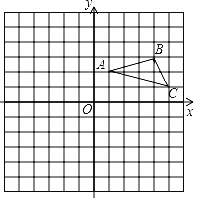
（1）如图3，在平面直角坐标系中，A（0，4），B（2，2），点C坐标为（﹣2，2），点C关于线段AB的视角为 度，x轴关于线段AB的视角为 度；
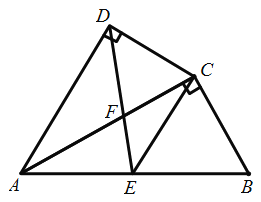
（2）如图4，点M是在x轴上，坐标为（2，0），过点M作线段EF⊥x轴，且EM＝MF＝1，当直线y＝kx（k≠0）关于线段EF的视角为90°，求k的值；
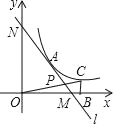
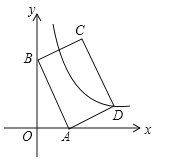
（3）如图5，在平面直角坐标系中，P（
，2），Q（+1，1），直线y＝ax+b（a＞0）与x轴的夹角为60°，且关于线段PQ的视角为45°，求这条直线的解析式．
【答案】（1）45，45；（2）k＝
；（3）y＝
x+﹣2
【解析】
（1）如图3，连接AC，则∠ABC=45°；设M是x轴的动点，当点M运动到点O时，∠AOB=45°，该视角最大，即可求解；
（2）如图4，以点M为圆心，长度1为半径作圆M，当圆与直线y=kx相切时，直线y=kx（k≠0）关于线段EF的视角为90°，即∠EQF=90°，则MQ⊥直线OE，OQ=1，OM=2，故直线的倾斜角为30°，即可求解；
（3）直线PQ的倾斜角为45°，分别作点Q、P作x轴、y轴的平行线交于点R，RQ=RP=1，以点R为圆心以长度1为半径作圆R，由（1）知，设直线与圆交于点Q′，由（1）知，当PQ′Q为等腰三角形时，视角为45°，则QQ=2RQ=2，故点Q′（-1，1），即可求解．
（1）如图3，连接AC，则∠ABC＝45°；
设M是x轴的动点，当点M运动到点O时，∠AOB＝45°，该视角最大，
由此可见：当△ABC为等腰三角形时，视角最大；
故答案为：45，45；
（2）如图4，以点M为圆心，长度1为半径作圆M，
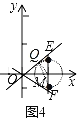
当圆与直线y＝kx相切时，直线y＝kx（k≠0）关于线段EF的视角为90°，即∠EQF＝90°，则MQ⊥直线OE，MQ＝1，OM＝2，故直线的倾斜角为30°，故k＝；
（3）直线PQ的倾斜角为45°，分别作点Q、P作x轴、y轴的平行线交于点R，RQ＝RP＝1，以点R为圆心以长度1为半径作圆R，
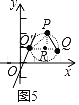
由（1）知，设直线与圆交于点Q′，由（1）知，当PQ′Q为等腰三角形时，视角为45°，
则QQ＝2RQ＝2，故点Q′（﹣1，1），
直线y＝ax+b（a＞0）与x轴的夹角为60°，则直线的表达式为：y＝x+b，
将点Q′的坐标代入上式并解得：
直线的表达式为：y＝x+﹣2
