题目内容
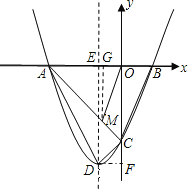
【题目】如图,在平面直角坐标系xoy中,抛物线y=x2向左平移1个单位,再向下平移4个单位,得到抛物线y=(x﹣h)2+k,所得抛物线与x轴交于A、B两点(点A在点B的左边),与y轴交于点C,顶点为D.

(1)求h、k的值;
(2)判断△ACD的形状,并说明理由;
(3)在线段AC上是否存在点M,使△AOM与△ABC相似?若存在,求出点M的坐标;若不存在,说明理由.
【答案】(1)h=﹣1,k=﹣4(2)△ACD是直角三角形;(3)见解析
【解析】
试题分析:(1)根据“左加右减,上加下减”的平移规律即可得到h、k的值;
(2)根据(1)题所得的抛物线的解析式,即可得到A、C、D的坐标,进而可求出AC、AD、CD的长,然后再判断△ACD的形状;
(3)易求得B点的坐标,即可得到AB、AC、OA的长;△AOM和△ABC中,已知的相等角是∠OAM=∠BAC,若两三角形相似,可考虑两种情况:
①∠AOM=∠ABC,此时OM∥BC,△AOM∽△ABC;②∠AOM=∠ACB,此时△AOM∽△ACB;
根据上述两种情况所得到的不同比例线段即可求出AM的长,进而可根据∠BAC的度数求出M点的横、纵坐标,即可得到M点的坐标.
解:(1)∵y=x2的顶点坐标为(0,0),
∴y=(x﹣h)2+k的顶点坐标D(﹣1,﹣4),
∴h=﹣1,k=﹣4 (3分)
(2)由(1)得y=(x+1)2﹣4
当y=0时,
(x+1)2﹣4=0
x1=﹣3,x2=1
∴A(﹣3,0),B(1,0)(1分)
当x=0时,y=(x+1)2﹣4=(0+1)2﹣4=﹣3
∴C点坐标为(0,﹣3)
又∵顶点坐标D(﹣1,﹣4)(1分)
作出抛物线的对称轴x=﹣1交x轴于点E
作DF⊥y轴于点F
在Rt△AED中,AD2=22+42=20
在Rt△AOC中,AC2=32+32=18
在Rt△CFD中,CD2=12+12=2
∵AC2+CD2=AD2
∴△ACD是直角三角形;
(3)存在.由(2)知,OA=3,OC=3,则△AOC为等腰直角三角形,∠BAC=45°;
连接OM,过M点作MG⊥AB于点G,
AC=![]()
①若△AOM∽△ABC,则![]() ,
,
即![]() ,AM=
,AM=![]()
∵MG⊥AB
∴AG2+MG2=AM2
∴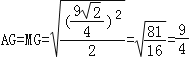
OG=AO﹣AG=3﹣![]()
∵M点在第三象限
∴M(![]() );
);
②若△AOM∽△ACB,则![]() ,
,
即![]() ,
,![]()
∴AG=MG=![]()
OG=AO﹣AG=3﹣2=1
∵M点在第三象限
∴M(﹣1,﹣2).
综上①、②所述,存在点M使△AOM与△ABC相似,且这样的点有两个,其坐标分别为(![]() ),(﹣1,﹣2).
),(﹣1,﹣2).