Question

【题目】如图，在平面直角坐标系xOy中，将二次函数的图象M沿x轴翻折，把所得到的图象向右平移2个单位长度后再向上平移8个单位长度，得到二次函数图象N．

（1）求N的函数表达式；

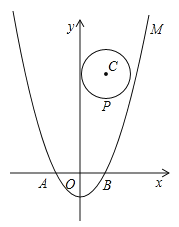
（2）设点P（m，n）是以点C（1，4）为圆心、1为半径的圆上一动点，二次函数的图象M与x轴相交于两点A、B，求的最大值；

（3）若一个点的横坐标与纵坐标均为整数，则该点称为整点．求M与N所围成封闭图形内（包括边界）整点的个数．

Answer 1

【答案】（1）；（2）；（3）25．

【解析】

试题分析：（1）根据二次函数N的图象是由二次函数M翻折、平移得到所以a=﹣1，求出二次函数N的顶点坐标即可解决问题．

（2）由=可知OP最大时，最大，求出OP的最大值即可解决问题．

（3）画出函数图象即可解决问题．

试题解析：（1）解：二次函数的图象M沿x轴翻折得到函数的解析式为，此时顶点坐标（0，1），将此图象向右平移2个单位长度后再向上平移8个单位长度得到二次函数图象N的顶点为（2，9），故N的函数表达式，即．

（2）∵A（﹣1，0），B（1，0），∴=

==，∴当PO最大时最大．如图，延长OC与⊙O交于点P，此时OP最大，∴OP的最大值=OC+PO=，∴最大值==．

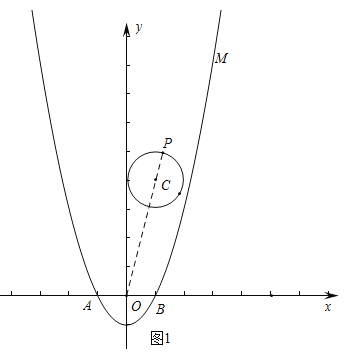
（3）M与N所围成封闭图形如图所示：

由图象可知，M与N所围成封闭图形内（包括边界）整点的个数为25个．