题目内容
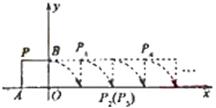
如图，边长为4的正方形OABC放置在平面直角坐标系中，OA在x轴正半轴上，OC在y轴正半轴上，当直线y=-x+b中的系数b从0开始逐渐变大时，在正方形上扫过的面积记为S．则S关于b的函数图象是
- A.
- B.
- C.
- D.
B
分析：当0≤b＜4；4≤b＜8；b＞8时，分别求出S，然后根据求得的解析式得到对应的函数图象即可找到正确选项．
解答：①当0≤b＜4，S=
•b2；
它的函数图象为抛物线的一部分，开口向上；
②当4≤b＜8，S=16-（8-b）2
=-（b-8）2+16，
它的函数图象为抛物线的一部分，开口向下；
③当b＞8，S=16；
它的函数图象为射线；
所以B选项正确．
故选B．
点评：本题考查了运用分类的思想求动点的函数图象的问题：分别求出每个时段的函数关系式，然后根据自变量和函数解析式作出相应的图象．
分析：当0≤b＜4；4≤b＜8；b＞8时，分别求出S，然后根据求得的解析式得到对应的函数图象即可找到正确选项．
解答：①当0≤b＜4，S=
•b2；它的函数图象为抛物线的一部分，开口向上；
②当4≤b＜8，S=16-
（8-b）2=-
（b-8）2+16，它的函数图象为抛物线的一部分，开口向下；
③当b＞8，S=16；
它的函数图象为射线；
所以B选项正确．
故选B．
点评：本题考查了运用分类的思想求动点的函数图象的问题：分别求出每个时段的函数关系式，然后根据自变量和函数解析式作出相应的图象．
练习册系列答案
阅读快车系列答案
相关题目
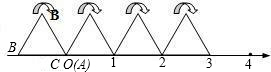
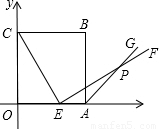
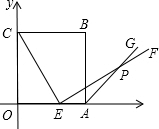如图，边长为6的正方OABC的顶点O在坐标原点处，点A、C分别在x轴、y轴的正半轴上，点E是OA边上的点（不与点A重合），EF⊥CE，且与正方形外角平分线AC交于点P．
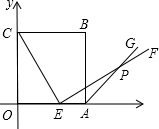如图，边长为6的正方OABC的顶点O在坐标原点处，点A、C分别在x轴、y轴的正半轴上，点E是OA边上的点（不与点A重合），EF⊥CE，且与正方形外角平分线AC交于点P．
轴正方向连续翻转2006次，点P依次落在点
，
，
，
，……
的位置，则
＝_________．
