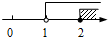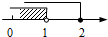题目内容
已知a、b、c均为实数，且a>b，c≠0，下列结论不一定正确的是
A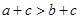． | B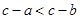． | C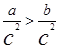． | D． |
D
分析：根据不等式的性质1，不等式两边同时加上或减去同一个数，不等号的方向不变；根据不等式的性质2，不等式两边同时乘以或除以同一个正数，不等号的方向不变；根据不等式的性质3，不等式两边同时乘以或除以同一个负数，不等号的方向改变；利用不等式的3个性质进行分析．
解答：解：A，根据不等式的性质一，不等式两边同时加上c，不等号的方向不变，故此选项正确；
B，∵a＞b，
∴-a＜-b，
∴-a+c＜-b+c，
故此选项正确；
C，∵c≠0，
∴c2＞0，
∵a＞b．
∴，
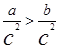故此选项正确；
D，∵a＞b，
a不知正数还是负数，
∴a2，与ab，的大小不能确定，故此选项错误；
故选：D
解答：解：A，根据不等式的性质一，不等式两边同时加上c，不等号的方向不变，故此选项正确；
B，∵a＞b，
∴-a＜-b，
∴-a+c＜-b+c，
故此选项正确；
C，∵c≠0，
∴c2＞0，
∵a＞b．
∴
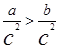，故此选项正确；
D，∵a＞b，
a不知正数还是负数，
∴a2，与ab，的大小不能确定，故此选项错误；
故选：D
练习册系列答案
相关题目
元．且购买5块A型小黑板和4块B型小黑板共需820元．
．请你通过计算，求出义洁中学从荣威公司购买A、B两种型号的小黑板有哪几种方案?
，并写出它的所有整数解．
．
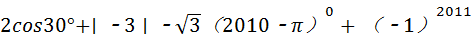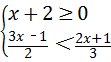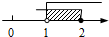
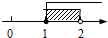
，并写出该不等式组的最小整数解．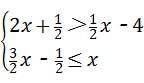
的解集在数轴上表示正确的是（ ）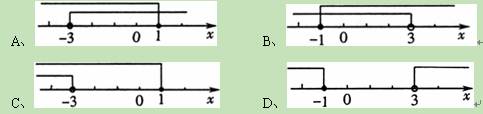
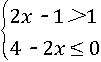的解在数轴上表示为（ ）
