题目内容
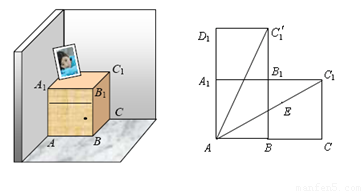
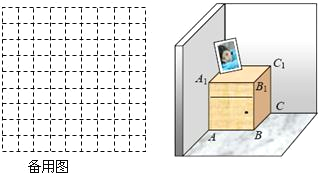 如图,一个长方体形的木柜放在墙角处(与墙面和地面均没有缝隙),有一只蚂蚁从柜角A处沿着木柜表面爬到柜角C1处.
如图,一个长方体形的木柜放在墙角处(与墙面和地面均没有缝隙),有一只蚂蚁从柜角A处沿着木柜表面爬到柜角C1处.(1)请你画出蚂蚁能够最快到达目的地的可能路径;
(2)当AB=4,BC=4,CC1=5时,求蚂蚁爬过的最短路径的长;
(3)求点B1到最短路径的距离.
分析:根据题意,先将长方体展开,再根据两点之间线段最短.
解答: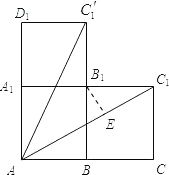 解:(1)如图,
解:(1)如图,
木柜的表面展开图是矩形ABC'1D1或ACC1A1.
故蚂蚁能够最快到达目的地的可能路径有如图的AC'1或AC1;(2分)
(2)蚂蚁沿着木柜表面矩形ABC'1D1爬过的路径AC'1的长是l1=
=
.(3分)
蚂蚁沿着木柜表面矩形矩形AB1C1D爬过的路径AC1的长=
,
蚂蚁沿着木柜表面ACC1A1爬过的路径AC1的长是l2=
=
.(4分)
l1>l2,故最短路径的长是l2=
.(5分)
(3)作B1E⊥AC1于E,
∵∠C1EB1=∠C1A1A,∠A1C1A是公共角,
∴△AA1C1∽△B1EC1,
即
=
,
则B1E=
•AA1=
•5=
为所求.(8分)
注:作垂线、相似(或等面积)、计算各(1分).
 解:(1)如图,
解:(1)如图,木柜的表面展开图是矩形ABC'1D1或ACC1A1.
故蚂蚁能够最快到达目的地的可能路径有如图的AC'1或AC1;(2分)
(2)蚂蚁沿着木柜表面矩形ABC'1D1爬过的路径AC'1的长是l1=
| 42+(4+5)2 |
| 97 |
蚂蚁沿着木柜表面矩形矩形AB1C1D爬过的路径AC1的长=
| 97 |
蚂蚁沿着木柜表面ACC1A1爬过的路径AC1的长是l2=
| (4+4)2+52 |
| 89 |
l1>l2,故最短路径的长是l2=
| 89 |
(3)作B1E⊥AC1于E,
∵∠C1EB1=∠C1A1A,∠A1C1A是公共角,
∴△AA1C1∽△B1EC1,
即
| B1E |
| AA1 |
| B1C1 |
| AC1 |
则B1E=
| B1C1 |
| AC1 |
| 4 | ||
|
| 20 |
| 89 |
| 89 |
注:作垂线、相似(或等面积)、计算各(1分).
点评:本题是一道趣味题,将长方体展开,根据两点之间线段最短,运用勾股定理解答即可.

练习册系列答案
 寒假学与练系列答案
寒假学与练系列答案
相关题目
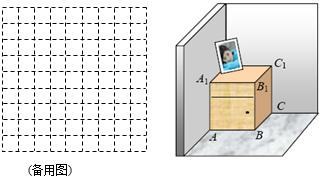
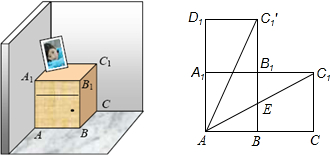 如图,一个长方体形的木柜放在墙角处(与墙面和地面均没有缝隙),有一只蚂蚁从柜角A处沿着木柜表面爬到柜角C1处.小明认为蚂蚁能够最快到达目的地的路径AC1,小王认为蚂蚁能够最快到达目的地的路径AC1′.已知AB=4,BC=4,CC1=5时,请你帮忙他们求出蚂蚁爬过的最短路径长.
如图,一个长方体形的木柜放在墙角处(与墙面和地面均没有缝隙),有一只蚂蚁从柜角A处沿着木柜表面爬到柜角C1处.小明认为蚂蚁能够最快到达目的地的路径AC1,小王认为蚂蚁能够最快到达目的地的路径AC1′.已知AB=4,BC=4,CC1=5时,请你帮忙他们求出蚂蚁爬过的最短路径长.