题目内容
(2005•新疆)在矩形ABCD中,AB=a,AD=2b(a>2b>0),E是AD的中点,BF⊥EC,垂足为F,求BF的长(用含有a、b的代数式表示).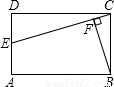
【答案】分析:根据矩形的性质,有了CD,DE的长,可在直角三角形CED中求出CE的长,然后用相似三角形CDE和BFC求出BF的长.
解答:解:在Rt△CDE中,根据勾股定理有:
CE=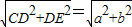 .
.
∵AD∥BC,
∴∠CED=∠BCF.
∵∠D=∠BFC=90°,
∴△CED∽△BCF,
∴ =
=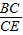 ,
,
∴BF= =
=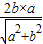 =
=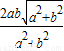 .
.
点评:本题主要考查了相似三角形的判定和性质以及勾股定理等知识点,根据相似三角形得出线段的比例关系是解题的关键.
解答:解:在Rt△CDE中,根据勾股定理有:
CE=
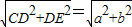 .
.∵AD∥BC,
∴∠CED=∠BCF.
∵∠D=∠BFC=90°,
∴△CED∽△BCF,
∴
 =
=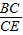 ,
,∴BF=
 =
=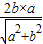 =
=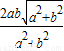 .
.点评:本题主要考查了相似三角形的判定和性质以及勾股定理等知识点,根据相似三角形得出线段的比例关系是解题的关键.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案 天天练口算系列答案
天天练口算系列答案
相关题目
 x+10,如果该弹簧最长可以拉伸到20cm,则它所挂物体的最大质量是 千克.
x+10,如果该弹簧最长可以拉伸到20cm,则它所挂物体的最大质量是 千克. x+10,如果该弹簧最长可以拉伸到20cm,则它所挂物体的最大质量是 千克.
x+10,如果该弹簧最长可以拉伸到20cm,则它所挂物体的最大质量是 千克.