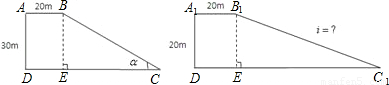
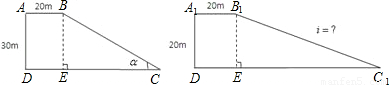
题目内容
 如图一段路基的横断面是梯形ABCD,高为3米,上底CD的宽是5米,AD面的坡比(指坡面的垂直高度与水平距离之比)为
如图一段路基的横断面是梯形ABCD,高为3米,上底CD的宽是5米,AD面的坡比(指坡面的垂直高度与水平距离之比)为| 3 |
分析:过D作DF⊥AB,CE⊥AB,则在Rt△ADF及Rt△CEB中可分别求出AF、BE,继而可得出AB,代入梯形的面积公式可得出横截面的面积.
解答:解:过D作DF⊥AB,CE⊥AB,
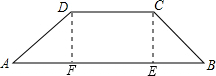
由题意得,DF=CE=3米,CD=5米,
∵AD面的坡比为
:2,
∴AF=2
米,
∵∠B=45°,
∴BE=CE=3米,
又∵EF=CD=5米,
∴AB=(2
+8)米,
∴S=
(5+8+2
)×3=(
+3
)m2.
答:路基下底AB的宽为(2
+8)米,横截面的面积为(
+3
)m2.

由题意得,DF=CE=3米,CD=5米,
∵AD面的坡比为
| 3 |
∴AF=2
| 3 |
∵∠B=45°,
∴BE=CE=3米,
又∵EF=CD=5米,
∴AB=(2
| 3 |
∴S=
| 1 |
| 2 |
| 3 |
| 39 |
| 2 |
| 3 |
答:路基下底AB的宽为(2
| 3 |
| 39 |
| 2 |
| 3 |
点评:本题考查了梯形及坡度坡角的知识,解答本题的关键是根据坡角的定义,在Rt△ADF中求出AF,另外要熟练掌握梯形的面积公式,难度一般.

练习册系列答案
 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案 ABC考王全优卷系列答案
ABC考王全优卷系列答案
相关题目
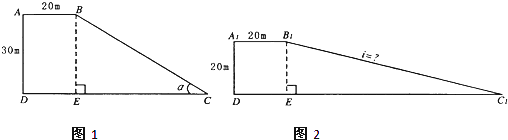
 如图一段路基的横断面是梯形ABCD,高为3米,上底CD的宽是5米,AD面的坡比(指坡面的垂直高度与水平距离之比)为
如图一段路基的横断面是梯形ABCD,高为3米,上底CD的宽是5米,AD面的坡比(指坡面的垂直高度与水平距离之比)为 ,∠B=45°,求路基下底AB的宽和横截面的面积.
,∠B=45°,求路基下底AB的宽和横截面的面积.