题目内容
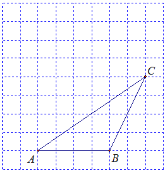
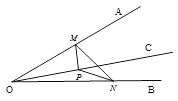
【题目】如图,∠AOB=30°,OC为∠AOB内部一条射线,点P为射线OC上一点,OP=4,点M、N分别为OA、OB边上动点,则△MNP周长的最小值为( )
A. 2 B. 4 C. ![]() D.
D. ![]()
【答案】B
【解析】
作点P关于OA的对称点P1,点P关于OB的对称点P2,连结P1P2,与OA的交点即为点M,与OB的交点即为点N,则此时M、N符合题意,求出线段P1P2的长即可.
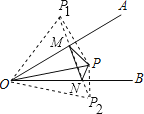
解:作点P关于OA的对称点P1,点P关于OB的对称点P2,连结P1P2,
与OA的交点即为点M,与OB的交点即为点N,此时△PMN的最小周长
∵点P关于OA的对称点为P1,关于OB的对称点为P2,连结OP1、OP2,
∴PM= P1M,OP=O P1,∠P1OA=∠POA;
∵点P关于OB的对称点为P2,
∴PN= P2N,OP=O P2,∠P2OB=∠POB,
∴OP1=OP2=OP=4,
∠P1OP2=∠P1OA+∠POA+∠POB+∠P2OB=2∠POA+2∠POB=2∠AOB=60°,
∴△OP1P2是等边三角形,
∴P1P2=OP1=4,
∴△PMN的最小周长为PM+MN+PN=P1M+MN+P2N=P1P2=4
即△PMN的周长的最小值是4.
故选:B.

【题目】某公司以每吨![]() 元的价格收购了
元的价格收购了![]() 吨某种药材,若直接在市场上销售,每吨的售价是
吨某种药材,若直接在市场上销售,每吨的售价是![]() 元.该公司决定加工后再出售,相关信息如下表所示:
元.该公司决定加工后再出售,相关信息如下表所示:
工艺 | 每天可加工药材的吨数 | 成品率 | 成品售价 (元/吨) |
粗加工 | 14 | 80% | 6000 |
精加工 | 6 | 60% | 11000 |
(注:①成品率80%指加工100吨原料能得到80吨可销售药材;②加工后的废品不产生效益.)
受市场影响,该公司必须在![]() 天内将这批药材加工完毕.
天内将这批药材加工完毕.
(1)若全部粗加工,可获利_______________________元;
(2)若尽可能多的精加工,剩余的直接在市场上销售,可获利_____________元;
(3)若部分粗加工,部分精加工,恰好![]() 天完成,求可获利多少元?
天完成,求可获利多少元?