题目内容
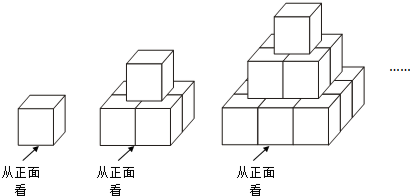
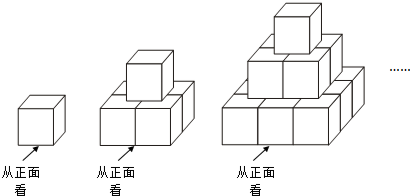
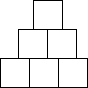
用棱长为1cm的若干小正方体按如图所示的规律在地面上搭建若个几何体.图中每个几何体自上而下分别叫第一层,第二层…第n层(n为正整数),其中第一层摆放一个,第二层摆放4个,第三层摆放9个…,依次按规律摆放.(图片所示为第三个几何体)
(1)求搭建第4个几何体的小立方体的个数,第n个几何体第n层的个数及总数.
(2)画出第2,第3个几何体的三视图,并求出这两个几何体的所有露出部分(不含底面)的面积之和.
(3)为了美观,若将几何体的露出部分都涂上油漆(不含底面),已知喷涂1cm2需要油漆0.1g,求喷涂第n个几何体,共需要多少g油漆?(用含n的代数式表示)
(1)求搭建第4个几何体的小立方体的个数,第n个几何体第n层的个数及总数.
(2)画出第2,第3个几何体的三视图,并求出这两个几何体的所有露出部分(不含底面)的面积之和.
(3)为了美观,若将几何体的露出部分都涂上油漆(不含底面),已知喷涂1cm2需要油漆0.1g,求喷涂第n个几何体,共需要多少g油漆?(用含n的代数式表示)

(1)搭建第4个几何体的小立方体的个数=1+4+9+16=30;第n个几何体第n层的个数为n2,其总数为1+22+32+42+…+n2;
(2)第2个几何体的主视图为
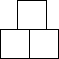
,左视图为
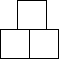
,俯视图为

;
第3个几何体的主视图为
,左视图为

,俯视图
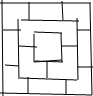
;
这两个几何体的所有露出部分(不含底面)的面积之和=4×3+4+4×6+9=49(cm2);
(3)第n个几何体的所有露出部分(不含底面)的面积=4×(1+2+3+…+n)+n2=4×
+n2=3n2+2n,
所以所需要的油漆量=(3n2+2n)×0.1=(0.3n2+0.2n)g.
(2)第2个几何体的主视图为

,左视图为

,俯视图为

;
第3个几何体的主视图为

,左视图为

,俯视图

;
这两个几何体的所有露出部分(不含底面)的面积之和=4×3+4+4×6+9=49(cm2);
(3)第n个几何体的所有露出部分(不含底面)的面积=4×(1+2+3+…+n)+n2=4×
| n(n+1) |
| 2 |
所以所需要的油漆量=(3n2+2n)×0.1=(0.3n2+0.2n)g.

练习册系列答案
相关题目