题目内容
若a、b、c是三角形三边的长,则代数式(a-b)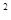 -c
-c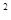 的值是( )
的值是( )
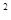 -c
-c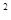 的值是( )
的值是( )| A.大于零 | B.小于零 |
| C.大于或等于零 | D.小于或等于零 |
B
分析:根据三角形任意两边之和大于第三边可得a+c>b,a<b+c,整理可得a+c-b>0,a-b-c<0,而(a-b)2-c2=(a-b+c)(a-b-c),那么可知乘积结果小于0.
解答:解:根据题意可得
a+c>b,a<b+c,
即a+c-b>0,a-b-c<0,
∵(a-b)2-c2=(a-b+c)(a-b-c),
∴(a-b)2-c2<0,
故选B.
解答:解:根据题意可得
a+c>b,a<b+c,
即a+c-b>0,a-b-c<0,
∵(a-b)2-c2=(a-b+c)(a-b-c),
∴(a-b)2-c2<0,
故选B.

练习册系列答案
 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案
相关题目

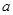 是同类项的是( )
是同类项的是( )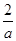 ;
;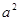 ;
;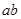 ;
; 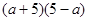 =__________。
=__________。  3·b4÷12a3b2 小题2:(2) (3x-1)(2x+3)-6x2
3·b4÷12a3b2 小题2:(2) (3x-1)(2x+3)-6x2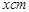 ,那么这个长方形的面积是( )
,那么这个长方形的面积是( )



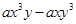
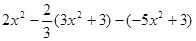 ,其中
,其中