题目内容
(1)在2006年元月的日历中(见下图1),任意圈出一竖列上相邻的三个数,设中间一个数为a,则用a的代数式表示这三个数(从小到大排列)分别是

(2)现将连续的自然数1至2006按图2的方式排成一个长方形陈列,用一个正方形框出9个数(见右图2).
①图2中框出的这9个数的和是
②有同学说:仿照①,图2中任意框出的9个数的和一定是中间一个数的9倍.你同意这种说法吗?为什么?
③在图2中,要使一个正方形框出的9个数的和分别等于2005,2007,你认为是否可能?如果有可能,请求出该正方形框出的9个数中的最大数和最小数;如果不可能,请说明理由.
a-7,a,a+7
a-7,a,a+7
.
(2)现将连续的自然数1至2006按图2的方式排成一个长方形陈列,用一个正方形框出9个数(见右图2).
①图2中框出的这9个数的和是
162
162
.②有同学说:仿照①,图2中任意框出的9个数的和一定是中间一个数的9倍.你同意这种说法吗?为什么?
③在图2中,要使一个正方形框出的9个数的和分别等于2005,2007,你认为是否可能?如果有可能,请求出该正方形框出的9个数中的最大数和最小数;如果不可能,请说明理由.
分析:(1)经过观察可知,如果中间的数是a,则上面的数是a-7,下面的数是a+7;
(2)①由10+11+12+17+18+19+24+25+26=162,即可得答案;
②设中间一个数是x,则另八个数为x-8,x-7,x-6,x-1,x+1,x+6,x+7,x+8,然后求得这9个数的和,即可证得任意框出的9个数的和一定是中间一个数的9倍;
③根据②,分别使9x=2005与9x=2007,解方程求得x的值,由x是整数,即可得到结论,又由最大数为(x+8)和最小数为(x-8)求得答案.
(2)①由10+11+12+17+18+19+24+25+26=162,即可得答案;
②设中间一个数是x,则另八个数为x-8,x-7,x-6,x-1,x+1,x+6,x+7,x+8,然后求得这9个数的和,即可证得任意框出的9个数的和一定是中间一个数的9倍;
③根据②,分别使9x=2005与9x=2007,解方程求得x的值,由x是整数,即可得到结论,又由最大数为(x+8)和最小数为(x-8)求得答案.
解答:解:(1)若中间的数是a,那么上面的数是a-7,下面的数是a+7.
故这三个数(从小到大排列)分别是a-7,a,a+7;
(2)①10+11+12+17+18+19+24+25+26=162;
②同意.
理由:设中间一个数是x,则另八个数为x-8,x-7,x-6,x-1,x+1,x+6,x+7,x+8,
则(x-8)+(x-7)+(x-6)+(x-1)+x+(x+1)+(x+6)+(x+7)+(x+8)=9x,
故任意框出的9个数的和一定是中间一个数的9倍.
(3)根据②可得:设中间一个数是x,则9个数的和为:9x,
若要使一个正方形框出的9个数的和等于2005,即9x=2005,
解得:x=222
,
故一若要使一个正方形框出的9个数的和等于2005,即9x=2007,
解得:x=223,
则最大数为:223+8=231,最小数为:223-8=215.
故答案为:(1)a-7,a,a+7,(2)①162.
故这三个数(从小到大排列)分别是a-7,a,a+7;
(2)①10+11+12+17+18+19+24+25+26=162;
②同意.
理由:设中间一个数是x,则另八个数为x-8,x-7,x-6,x-1,x+1,x+6,x+7,x+8,
则(x-8)+(x-7)+(x-6)+(x-1)+x+(x+1)+(x+6)+(x+7)+(x+8)=9x,
故任意框出的9个数的和一定是中间一个数的9倍.
(3)根据②可得:设中间一个数是x,则9个数的和为:9x,
若要使一个正方形框出的9个数的和等于2005,即9x=2005,
解得:x=222
| 7 |
| 9 |
故一若要使一个正方形框出的9个数的和等于2005,即9x=2007,
解得:x=223,
则最大数为:223+8=231,最小数为:223-8=215.
故答案为:(1)a-7,a,a+7,(2)①162.
点评:此题考查了一元一次方程的应用.此题属于规律性题目,难度适中,集体的关键是找到规律:设中间一个数是x,则另八个数为x-8,x-7,x-6,x-1,x+1,x+6,x+7,x+8.

练习册系列答案
 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目

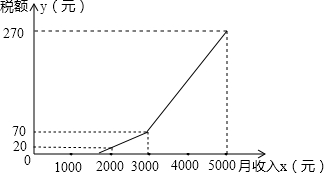 得税缴纳情况.
得税缴纳情况.