题目内容
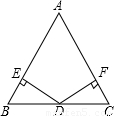
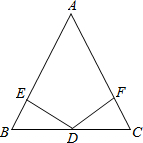如图DE⊥AB，DF⊥AC，垂足分别为E、F，请你从（1）AB=AC；（2）BD=CD；（3）DE=DF中选出两个作为已知条件，另一个作为结论，编写一个几何证明题并完成证明过程．已知：DE⊥AB，DF⊥AC，垂足分别为E、F，且
AB=AC
AB=AC
，BD=DC
BD=DC
求证：
DE=DF
DE=DF
证明：
略
略
．分析：可以选（1）AB=AC；（2）BD=CD两个作为已知条件，（3）DE=DF作为结论．先根据垂直的定义得到∠DEB=∠DFC=90°，再根据等腰三角形的性质由AB=AC得到∠B=∠C，然后利用“AAS”可证明△DEB≌△DFC，则根据全等的性质可得DE=DF．
解答：解：选（1）AB=AC；（2）BD=CD两个作为已知条件，（3）DE=DF作为结论．
证明如下：
∵DE⊥AB，DF⊥AC，
∴∠DEB=∠DFC=90°，
∵AB=AC，
∴∠B=∠C，
∵在△DEB和△DFC中
，
∴△DEB≌△DFC（AAS），
∴DE=DF．
证明如下：
∵DE⊥AB，DF⊥AC，
∴∠DEB=∠DFC=90°，
∵AB=AC，
∴∠B=∠C，
∵在△DEB和△DFC中
|
∴△DEB≌△DFC（AAS），
∴DE=DF．
点评：本题考查了全等三角形的判定与性质：判定三角形全等的方法有“SSS”、“SAS”、“ASA”、“AAS”；全等三角形的对应边相等．也考查了等腰三角形的性质．
练习册系列答案
相关题目
22、（A类）如图DE⊥AB，DF⊥AC，垂足分别为E，F，请你从下面三个条件中，再选出两个作为已知条件，另一个为结论，推出一个正确的命题（只需写出一种情况）．
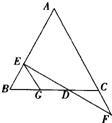
如图DE⊥AB，DF⊥AC，垂足分别为E、F，请你从（1）AB=AC；（2）BD=CD；（3）DE=DF中选出两个作为已知条件，另一个作为结论，编写一个几何证明题并完成证明过程．
