题目内容
【题目】如图,在△ABC中,∠C=90°,∠BAC=30°,AB=8,AD平分∠BAC,点PQ分别是AB、AD边上的动点,则PQ+BQ的最小值是

A. 4 B. 5 C. 6 D. 7
【答案】A
【解析】
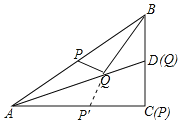
如图,作点P关于直线AD的对称点P′,连接QP′,由△AQP≌△AQP′,得PQ=QP′,欲求PQ+BQ的最小值,只要求出BQ+QP′的最小值,即当BP′⊥AC时,BQ+QP′的值最小,此时Q与D重合,P′与C重合,最小值为BC的长.
如图,作点P关于直线AD的对称点P′,连接QP′,
在△AQP和△AQP′中,
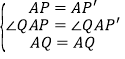 ,
,
∴△AQP≌△AQP′,
∴PQ=QP′
∴欲求PQ+BQ的最小值,只要求出BQ+QP′的最小值,
∴当BP′⊥AC时,BQ+QP′的值最小,此时Q与D重合,P′与C重合,最小值为BC的长。
在Rt△ABC中,∵∠C=90°,AB=8,∠BAC=30°,
∴BC=![]() AB=4,
AB=4,
∴PQ+BQ的最小值是4,
故选A.

练习册系列答案
相关题目