题目内容
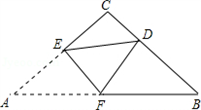
选做题已知如图,△ABC为直角三角形纸片,∠C=90°,AC≤BC,将纸片沿EF折叠,使A点
 落在BC上D点,若△DCE和△FBD都是等腰三角形,
落在BC上D点,若△DCE和△FBD都是等腰三角形,(1)则∠B=
(2)若△DFE和△FBD都是等腰三角形,求∠B.
分析:首先确定△BDF不是以DF=BF为腰的等腰三角形,由折叠的性质可得DF=AF,如果DF=FB,那么则可得DF=AF=FB,这是不可能的,如果AF=FB,那么应该满足CF=AF=FB,而CF≠DF,故这种情况不可能.
(1)由△DEC是等腰三角形可得出∠CED=∠CDE=45°,设∠B=x,①若BD=BF,可得∠BDF=∠BFD=
(180°-x),继而可得出∠EDF=∠A的度数,根据∠A+∠B=90°可解出x.②若DF=BD,可得∠EDF=∠A=2x-45°,根据∠A+∠B=90°可解出x.
(2)分情况进行讨论,①AE=AF,DF=DB,②AE=AF,BD=BF,③EA=EF,DF=DB,④EA=EF,BD=BF,⑤FE=FA,DF=DB,⑥FE=FA,BD=BF,这几种情况下,分别表示出∠B及∠EFA,的度数,利用平角AFB等于180°列方程可得出答案.
(1)由△DEC是等腰三角形可得出∠CED=∠CDE=45°,设∠B=x,①若BD=BF,可得∠BDF=∠BFD=
| 1 |
| 2 |
(2)分情况进行讨论,①AE=AF,DF=DB,②AE=AF,BD=BF,③EA=EF,DF=DB,④EA=EF,BD=BF,⑤FE=FA,DF=DB,⑥FE=FA,BD=BF,这几种情况下,分别表示出∠B及∠EFA,的度数,利用平角AFB等于180°列方程可得出答案.
解答: 解:(1)①若BD=BF,
解:(1)①若BD=BF,
由△DEC是等腰三角形可得出∠CED=∠CDE=45°,
设∠B=x,可得∠BDF=∠BFD=
(180°-x),
∴∠EDF=45°+
x=∠A,
又∵∠A+∠B=90°,
∴45°+
x+x=90°,
解得:x=30°.即此时∠B=30°.
②若DF=BD,
则∴∠EDF=2x-45°=∠A,
∴2x-45°+x=90°,
解得:x=45°.
(2)设∠B=x,
①AE=AF,DF=DB,
则∠DFB=∠B=x,∠A=90°-x,
∴∠AEF=∠AFE=∠EFD=
,
则x+2×
=180°,解得x=45°;
②AE=AF,BD=BF,则∠AEF=∠AFE=∠EFD=
,∠DFB=
,
则
+2×
=180°,解得x=0,不符合题意;
③EA=EF,DF=DB,则∠A=∠EFA=90°-x,∠DFB=∠B=x,
则2(90°-x)+x=180°,解得x=0,不符合题意;
④EA=EF,BD=BF,则∠A=∠EFA=90°-x,∠DFB=
,
则2(90°-x)+
=180°,解得x=36°.
⑤FE=FA,DF=DB,则∠EFA=2x,∠DFB=∠B=x,
则5x=180°,解得x=36°;
⑥FE=FA,BD=BF,则∠EFA=2x,∠DFB=
,
则4x+
=180°,解得x=
°.
综上可得∠B=45°或36°或
°.
 解:(1)①若BD=BF,
解:(1)①若BD=BF,由△DEC是等腰三角形可得出∠CED=∠CDE=45°,
设∠B=x,可得∠BDF=∠BFD=
| 1 |
| 2 |
∴∠EDF=45°+
| 1 |
| 2 |
又∵∠A+∠B=90°,
∴45°+
| 1 |
| 2 |
解得:x=30°.即此时∠B=30°.
②若DF=BD,
则∴∠EDF=2x-45°=∠A,
∴2x-45°+x=90°,
解得:x=45°.
(2)设∠B=x,
①AE=AF,DF=DB,
则∠DFB=∠B=x,∠A=90°-x,
∴∠AEF=∠AFE=∠EFD=
| 90°+x |
| 2 |
则x+2×
| 90°+x |
| 2 |
②AE=AF,BD=BF,则∠AEF=∠AFE=∠EFD=
| 90°+x |
| 2 |
| 180°-x |
| 2 |
则
| 180°-x |
| 2 |
| 90°+x |
| 2 |
③EA=EF,DF=DB,则∠A=∠EFA=90°-x,∠DFB=∠B=x,
则2(90°-x)+x=180°,解得x=0,不符合题意;
④EA=EF,BD=BF,则∠A=∠EFA=90°-x,∠DFB=
| 180°-x |
| 2 |
则2(90°-x)+
| 180°-x |
| 2 |
⑤FE=FA,DF=DB,则∠EFA=2x,∠DFB=∠B=x,
则5x=180°,解得x=36°;
⑥FE=FA,BD=BF,则∠EFA=2x,∠DFB=
| 180°-x |
| 2 |
则4x+
| 180°-x |
| 2 |
| 180 |
| 7 |
综上可得∠B=45°或36°或
| 180 |
| 7 |
点评:本题考查了翻折变换及等腰三角形的性质,难度较大,难点在于不确定等腰三角形的腰,需要分情况进行讨论,尤其是第二问需要分六种情况,注意讨论的时候按次序进行,避免漏解.

练习册系列答案
相关题目
 索∠PAC,∠APB,∠PBD之间的关系又是如何?
索∠PAC,∠APB,∠PBD之间的关系又是如何?