题目内容
先阅读,后填空.从某校参加初中毕业考试的学生中,抽取了30名学生的数学成绩,分数如下:
90,85,84,86,87,98,79,85,90,93,68,95,85,71,78,61,94,88,77,100,70,97,85,68,99,88,85,92,93,97.
这个样本数据的频率分布表如下:
| 分组 | 频数累计 | 频数 | 频率 |
| 59.5-64.5 | - | 1 | 0.033 |
| 64.5-69.5 | T | 2 | 0.067 |
| 69.5-74.5 | 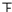 | 2 | 0.067 |
| 74.5-79.5 | 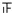 | 3 | |
| 79.5-84.5 | - | 1 | 0.033 |
| 84.5-89.5 | 正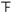 | 9 | 0.300 |
| 89.5-94.5 | 正- | 6 | 0.200 |
| 94.5-99.5 | 正 | 0.167 | |
| 99.5-104.5 | - | 1 | 0.033 |
| 合计 | 30 | 1.000 |
(1)这个样本数据的众数是______.
(2)列频率分布表时,所取的组距为______.
(3)在这个频率分布表中,数据落在94.5~99.5(分)范围内的频数为______.
(4)在这个频率分布表中,数据落在74.5~79.5(分)范围内的频率为______.
(5)在这个频率分布表中,频率最大的一组数据的范围是______.
(6)估计这个学校初中毕业考试的数学成绩在80分以上的约占______%.
【答案】分析:(1)根据众数的定义填空即可;
(2)由每个组的最大值和最小值的差即可求出所取的组距;
(3)找到数据落在94.5~99.5(分)范围内的个数即为频数;
(4)找到在这个频率分布表中,数据落在74.5~79.5(分)范围内的频数,进而求出其频率;
(5)在这个频率分布表中,找到频数最多的则频率最大的一组数据的范围可求;
(6)求出3个学生中80以上的成绩所占百分数则可以估计这个学校初中毕业考试的数学成绩在80分以上的约占的百分数
解答:解:(1)因为85这一个数据出现次数最多,所以众数是85;
(2)因为64.5-59.5=5,所以列频率分布表时,所取的组距为5;
(3)数据落在94.5~99.5(分)范围内的频数为5;
(4)数据落在74.5~79.5(分)范围内的频数是3,所以频率=3÷30=0.100;
(5)在这个频率分布表中,频数最多是84.5~89.5;则频率是最大的一组
(6)30个学生的数学成绩中,80以上的22人,所以估计这个学校初中毕业考试的数学成绩在80分以上的约占的百分数为22÷30×100%≈73.3%.
故答案为:85;5;5;0.100;84.5~89.5;73.3.
点评:本题考查了频数(率)分布表,要认真分析数据,要充分运用数形结合思想来解决由统计图形式给出的数学实际问题.同时掌握频率、众数的概念以及用样本估计总体.
(2)由每个组的最大值和最小值的差即可求出所取的组距;
(3)找到数据落在94.5~99.5(分)范围内的个数即为频数;
(4)找到在这个频率分布表中,数据落在74.5~79.5(分)范围内的频数,进而求出其频率;
(5)在这个频率分布表中,找到频数最多的则频率最大的一组数据的范围可求;
(6)求出3个学生中80以上的成绩所占百分数则可以估计这个学校初中毕业考试的数学成绩在80分以上的约占的百分数
解答:解:(1)因为85这一个数据出现次数最多,所以众数是85;
(2)因为64.5-59.5=5,所以列频率分布表时,所取的组距为5;
(3)数据落在94.5~99.5(分)范围内的频数为5;
(4)数据落在74.5~79.5(分)范围内的频数是3,所以频率=3÷30=0.100;
(5)在这个频率分布表中,频数最多是84.5~89.5;则频率是最大的一组
(6)30个学生的数学成绩中,80以上的22人,所以估计这个学校初中毕业考试的数学成绩在80分以上的约占的百分数为22÷30×100%≈73.3%.
故答案为:85;5;5;0.100;84.5~89.5;73.3.
点评:本题考查了频数(率)分布表,要认真分析数据,要充分运用数形结合思想来解决由统计图形式给出的数学实际问题.同时掌握频率、众数的概念以及用样本估计总体.

练习册系列答案
相关题目


