题目内容
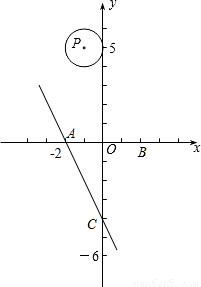
(2002•咸宁)已知经过(-3,5),(-1,-3),(0,-4)三点的抛物线与x轴交于A、B两点(A点在B点的左边),顶点为C.(1)求这条抛物线的解析式;
(2)求点A、B的坐标及直线CB的解析式;
(3)设点P(a,0)为x轴上一动点,那么以P点为圆心,2为半径的⊙P与直线CB有哪几种位置关系?并求出相应位置关系时a的取值范围.

【答案】分析:(1)根据已知的抛物线上的三点坐标,可用待定系数法求出抛物线的解析式.
(2)根据(1)得出的抛物线的解析式即可求出A、B的坐标,然后用待定系数法可求出直线BC的解析式.
(3)直线与圆的位置关系无非是相切、相交、相离这三种情况,本题中,只需求出圆P与直线BC相切时P点的坐标即可.然后根据此时a的值,即可判断出圆与直线的三种位置关系中a的取值范围.
解答:解:(1)设抛物线的解析式为y=ax2+bx+c,由题意,
得: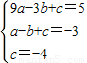 ,
,
解得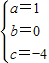 ,
,
∴抛物线的解析式为y=x2-4.
(2)由(1)的抛物线可知:当y=0时,x2-4=0,
解得x=2,x=-2
∵A点在B点的左边
∴A(-2,0),B(2,0).
设直线BC的解析式为y=kx-4,已知直线过B(2,0),则有:
2k-4=0,k=2
∴直线BC的解析式为y=2x-4.
(3)当a<2-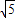 或a>2+
或a>2+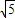 时,⊙P与直线BC相离;
时,⊙P与直线BC相离;
当a=2±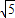 时,⊙P与直线BC相切;
时,⊙P与直线BC相切;
当2-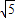 <a<2+
<a<2+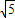 时,⊙P与直线BC相交.
时,⊙P与直线BC相交.
点评:本题主要考查二次函数和一次函数解析式的确定、直线与圆的位置关系等知识.
(2)根据(1)得出的抛物线的解析式即可求出A、B的坐标,然后用待定系数法可求出直线BC的解析式.
(3)直线与圆的位置关系无非是相切、相交、相离这三种情况,本题中,只需求出圆P与直线BC相切时P点的坐标即可.然后根据此时a的值,即可判断出圆与直线的三种位置关系中a的取值范围.
解答:解:(1)设抛物线的解析式为y=ax2+bx+c,由题意,
得:
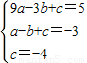 ,
,解得
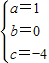 ,
,∴抛物线的解析式为y=x2-4.
(2)由(1)的抛物线可知:当y=0时,x2-4=0,
解得x=2,x=-2
∵A点在B点的左边
∴A(-2,0),B(2,0).
设直线BC的解析式为y=kx-4,已知直线过B(2,0),则有:
2k-4=0,k=2
∴直线BC的解析式为y=2x-4.
(3)当a<2-
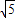 或a>2+
或a>2+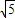 时,⊙P与直线BC相离;
时,⊙P与直线BC相离;当a=2±
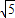 时,⊙P与直线BC相切;
时,⊙P与直线BC相切;当2-
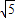 <a<2+
<a<2+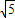 时,⊙P与直线BC相交.
时,⊙P与直线BC相交.点评:本题主要考查二次函数和一次函数解析式的确定、直线与圆的位置关系等知识.

练习册系列答案
 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案
相关题目