题目内容
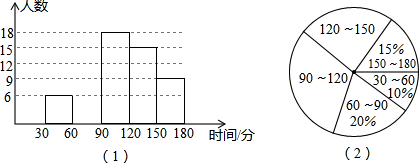
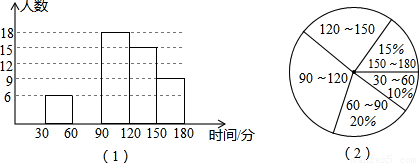
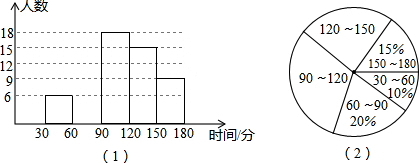
某中学对本校学生每天完成作业所用时间的情况进行抽样调查,随机调查了九年级部分学生每天完成作业所用的时间,并把统计结果制作成如图所示的频数分布直方图(时间取整数,图中从左至右依次为第一、二、三、四、五组)和扇形统计图.请结合图中信息解答下列问题.(1)本次调查的学生人数为______人;
(2)补全频数分布直方图;
(3)根据图形提供的信息判断,下列结论正确的是______(只填所有正确结论的代号);
A.由图(1)知,学生完成作业所用时间的中位数在第三组内
B.由图(1)知,学生完成作业所用时间的众数在第三组内
C.图(2)中,90~120数据组所在扇形的圆心角为108°
D.图(1)中,落在第五组内数据的频率为0.15
(4)学生每天完成作业时间不超过120分钟,视为课业负担适中.根据以上调查,估计该校九年级560名学生中,课业负担适中的学生约有多少人?

【答案】分析:(1)根据完成课外作业时间低于60分钟的学生数占被调查人数的10%.可求出抽查的学生人数;
(2)根据总人数,现有人数为补上那12人,画图即可;
(3)根据中位数、众数、频率的意义对各选项依次进行判断即可解答;
(4)先求出60人里学生每天完成课外作业时间在120分钟以下的人的比例,再按比例估算全校的人数.
解答:解:(1)6÷10%=60(人).
(2)补全的频数分布直方图如图所示:

(3)A.由图(1)知,学生完成作业所用时间的中位数在第三组内,正确;
B.由图(1)知,学生完成作业所用时间的众数不在第三组内,错误;
C.图(2)中,90~120数据组所在扇形的圆心角为108°.正确;
D.图(1)中,落在第五组内数据的频率为0.15,正确.
故答案为:60;ACD.
(4) =
=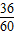 =60%,即样本中,完成作业时间不超过120分钟的学生占60%.
=60%,即样本中,完成作业时间不超过120分钟的学生占60%.
∴560×60%=336.
答:九年级学生中,课业负担适中的学生约为336人.
点评:本题考查读频数分布直方图的能力和利用统计图获取信息的能力.同时考查中位数、众数的求法:给定n个数据,按从小到大排序,如果n为奇数,位于中间的那个数就是中位数;如果n为偶数,位于中间两个数的平均数就是中位数.任何一组数据,都一定存在中位数的,但中位数不一定是这组数据量的数.给定一组数据,出现次数最多的那个数,称为这组数据的众数.
(2)根据总人数,现有人数为补上那12人,画图即可;
(3)根据中位数、众数、频率的意义对各选项依次进行判断即可解答;
(4)先求出60人里学生每天完成课外作业时间在120分钟以下的人的比例,再按比例估算全校的人数.
解答:解:(1)6÷10%=60(人).
(2)补全的频数分布直方图如图所示:

(3)A.由图(1)知,学生完成作业所用时间的中位数在第三组内,正确;
B.由图(1)知,学生完成作业所用时间的众数不在第三组内,错误;
C.图(2)中,90~120数据组所在扇形的圆心角为108°.正确;
D.图(1)中,落在第五组内数据的频率为0.15,正确.
故答案为:60;ACD.
(4)
 =
=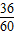 =60%,即样本中,完成作业时间不超过120分钟的学生占60%.
=60%,即样本中,完成作业时间不超过120分钟的学生占60%.∴560×60%=336.
答:九年级学生中,课业负担适中的学生约为336人.
点评:本题考查读频数分布直方图的能力和利用统计图获取信息的能力.同时考查中位数、众数的求法:给定n个数据,按从小到大排序,如果n为奇数,位于中间的那个数就是中位数;如果n为偶数,位于中间两个数的平均数就是中位数.任何一组数据,都一定存在中位数的,但中位数不一定是这组数据量的数.给定一组数据,出现次数最多的那个数,称为这组数据的众数.

练习册系列答案
相关题目
 ,估计该校九年级560名学生中,课业负担适中的学生约有多少人?
,估计该校九年级560名学生中,课业负担适中的学生约有多少人?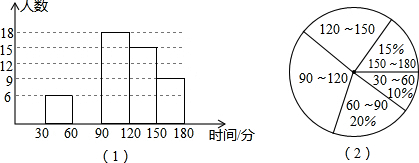 ,估计该校九年级560名学生中,课业负担适中的学生约有多少人?
,估计该校九年级560名学生中,课业负担适中的学生约有多少人?