题目内容
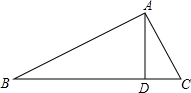（2011•长宁区一模）已知：如图，AD是△ABC的边BC上的高，且AD是BD与DC的比例中项．求证：△ABC是直角三角形．分析：由AD是BD与DC的比例中项，根据比例中项的性质，即可得AD2=BD•BC，∠B=∠B，可知△ABD∽△CAD，由AD是△ABC的边BC上的高，则可求得∠BAC=90°，故△ABC是直角三角形．
解答：证明：∵AD是BD与DC的比例中项，
∴AD2=BD•DC，
∴
=
，
∵AD是△ABC的边BC上的高，
∴∠ADB=∠CDA=90°，
∴△ABD∽△CAD，
∴∠B=∠CAD，
∴∠BAC=∠BAD+∠CAD=∠BAD+∠B=90°，
∴△ABC是直角三角形．
∴AD2=BD•DC，
∴
| AD |
| BD |
| DC |
| AD |
∵AD是△ABC的边BC上的高，
∴∠ADB=∠CDA=90°，
∴△ABD∽△CAD，
∴∠B=∠CAD，
∴∠BAC=∠BAD+∠CAD=∠BAD+∠B=90°，
∴△ABC是直角三角形．
点评：此题考查了相似三角形的判定与性质．此题难度不大，解题的关键是注意数形结合思想的应用．
练习册系列答案
阅读快车系列答案
相关题目
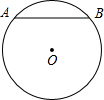（2011•长宁区一模）已知⊙O的半径是5cm．弦AB=8cm．
（2011•长宁区一模）如图，在直角坐标系中，∠α的顶点与坐标原点O重合，一边在x轴正半轴上，另一边是射线OM．已知cotα=