题目内容
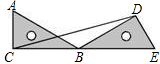
 33、如图所示,把一个直角三角尺ABC绕着60°角的顶点B顺时针旋转,使得点C与AB的延长线上的点D重合,已知BC=6.
33、如图所示,把一个直角三角尺ABC绕着60°角的顶点B顺时针旋转,使得点C与AB的延长线上的点D重合,已知BC=6.(1)三角尺旋转了多少度?连接CD,试判断△BCD的形状;
(2)求AD的长;
(3)连接CE,试猜想线段AC与CE的大小关系,并证明你的结论.
分析:(1)由直角三角尺ABC绕着60°角的顶点B顺时针旋转,点C与AB的延长线上的点D重合,根据旋转的性质得BD=BC,∠DBC等于旋转角,且∠DBC=180°-60°=120°,即可判断所三角尺旋转的度数,△BCD的形状;
(2)由三角尺ABC为直角三角形,∠ACB=90°,∠A=30°,得到AB=2BC=2×6=12,而BD=BC,即可得到AD=AB+BD的长;
(3)连接CE,△BCD为等腰三角形,由∠CBE=180°-(∠ABC+∠EBD)=60°=∠DBE,根据等腰三角形的性质得到BE垂直平分底边CD,则CE=DE,即可得到AC=CE.
(2)由三角尺ABC为直角三角形,∠ACB=90°,∠A=30°,得到AB=2BC=2×6=12,而BD=BC,即可得到AD=AB+BD的长;
(3)连接CE,△BCD为等腰三角形,由∠CBE=180°-(∠ABC+∠EBD)=60°=∠DBE,根据等腰三角形的性质得到BE垂直平分底边CD,则CE=DE,即可得到AC=CE.
解答:解:(1)∵直角三角尺ABC绕着60°角的顶点B顺时针旋转,点C与AB的延长线上的点D重合,
∴BD=BC,∠DBC等于旋转角,且∠DBC=180°-60°=120°,
∴三角尺旋转了120度,△BCD为等腰三角形;
(2)∵三角尺ABC为直角三角形,∠ACB=90°,∠A=30°,
∴AB=2BC=2×6=12,
∵BD=BC,A、B、D三点在一直线上,
∴AD=AB+BD=12+6=18;
(3)如图,连接CE,则AC=CE.

证明如下:
∵BC=BD,
即△BCD为等腰三角形,
又∵∠EBD=∠ABC=60°,
而点A、B、D在一条直线上,
∴∠CBE=180°-(∠ABC+∠EBD)=60°=∠DBE,
即BE平分等腰△BCD的顶角,
∴BE垂直平分底边CD,
∴CE=DE,
而DE=AC
所以AC=CE.
∴BD=BC,∠DBC等于旋转角,且∠DBC=180°-60°=120°,
∴三角尺旋转了120度,△BCD为等腰三角形;
(2)∵三角尺ABC为直角三角形,∠ACB=90°,∠A=30°,
∴AB=2BC=2×6=12,
∵BD=BC,A、B、D三点在一直线上,
∴AD=AB+BD=12+6=18;
(3)如图,连接CE,则AC=CE.

证明如下:
∵BC=BD,
即△BCD为等腰三角形,
又∵∠EBD=∠ABC=60°,
而点A、B、D在一条直线上,
∴∠CBE=180°-(∠ABC+∠EBD)=60°=∠DBE,
即BE平分等腰△BCD的顶角,
∴BE垂直平分底边CD,
∴CE=DE,
而DE=AC
所以AC=CE.
点评:本题考查了旋转的性质:旋转前后的两个图形全等,对应点与旋转中心的连线段的夹角等于旋转角,对应点到旋转中心的距离相等.也考查了含30度的直角三角形三边的关系以及等腰三角形的性质.

练习册系列答案
相关题目
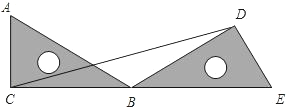 使得点A与CB的延长线上的点E重合.
使得点A与CB的延长线上的点E重合. 24、如图所示,把一个直角三角尺ABC绕着60°角的顶点B顺时针旋转,使得点C与AB的延长线上的点D重合.
24、如图所示,把一个直角三角尺ABC绕着60°角的顶点B顺时针旋转,使得点C与AB的延长线上的点D重合. 如图所示,把一个直角三角尺ABC绕着60°角的顶点B顺时针旋转,使得点C与AB的延长线上的点D重合,已知BC=8.
如图所示,把一个直角三角尺ABC绕着60°角的顶点B顺时针旋转,使得点C与AB的延长线上的点D重合,已知BC=8.