题目内容
下列命题:①连接四边形各边中点所得四边形为矩形,那么原四边形一定为菱形;②一直角三角形的两边长为3和4,则斜边上的中线长为2.5;③对我国首架大型民用直升机各零部件的检查,适宜采用全面调查(普查)方式;④化简:
(m≠n)=1.其中真命题的个数有( )
| 1 |
| m-n |
| m2-2mn+n2 |
| A、1个 | B、2个 | C、3个 | D、4个 |
分析:①根据题意,画出图形,证明不成立即可;②两边长为3和4,分两种情况:第一是两直角边长为3和4;第二是一条直角边长为3和斜边长为4;③对我国首架大型民用直升机各零部件的检查,需要收集的数据全面、准确;④根据分式的化简,计算出即可.
解答: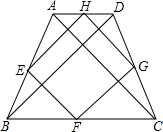 解:
解:
①如图,在梯形ABCD中,AC⊥BD,E、F、G、H是梯形各边的中点
∴四边形EFGH是矩形;故本项错误;
②当两直角边长为3和4时,斜边长为5,
所以,斜边上的中线长为2.5;
当一条直角边长为3和斜边长为4时,
所以,斜边上的中线长为2;故本项错误;
③根据对我国首架大型民用直升机各零部件的检查,需要收集到的数据全面、准确,
所以,适宜采用全面调差方式;故本项正确;
④当m>n时,原式=
×(m-n)=1;
当m<n时,原式=
×(n-m)=-1;
故本项错误.
综上,正确的命题有1个.
故选A.
 解:
解:①如图,在梯形ABCD中,AC⊥BD,E、F、G、H是梯形各边的中点
∴四边形EFGH是矩形;故本项错误;
②当两直角边长为3和4时,斜边长为5,
所以,斜边上的中线长为2.5;
当一条直角边长为3和斜边长为4时,
所以,斜边上的中线长为2;故本项错误;
③根据对我国首架大型民用直升机各零部件的检查,需要收集到的数据全面、准确,
所以,适宜采用全面调差方式;故本项正确;
④当m>n时,原式=
| 1 |
| m-n |
当m<n时,原式=
| 1 |
| m-n |
故本项错误.
综上,正确的命题有1个.
故选A.
点评:本题考查了菱形的性质、矩形的判定、解直角三角形、全面调查与抽样调查,本题综合性较强,用到的知识较多,考查了学生综合运用知识的能力.

练习册系列答案
 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案
相关题目