题目内容
【题目】在等腰△ABC中，AB=BC=5，AC=8，点E、F分别是AC、AB上的动点，将△AEF折叠，使点A落在△ABC的边AC上点A′处（A′不与点A重合），当△A′BC为等腰三角形时，AE的长为_______．
【答案】
或
【解析】
由勾股定理求出AB，设AE=x，则A'E=x，A'C=8﹣2x；分三种情况讨论：
①当A'B=A'C时，证明三角形相似可得结论；
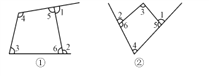
②当BC=A'C时，如图2，列出方程，解方程即可；
③当A'B=BC时，A与A'重合，此种情况不成立．
由翻折变换的性质得：AE=A'E，∠AEF=∠A'EF=90°．
∵AC=8，BC=6，设AE=A'E=x，则A'C=8﹣2x；
分三种情况讨论：
①当A'B=A'C时，如图1，∠C=∠A=∠CBA'，∴△CA'B∽△CBA，∴
，∴
，x=，∴AE=；
②当BC=A'C时，如图2，则8﹣2x=5，解得：x=，∴AE=；
③当A'B=BC时，A与A'重合，此种情况不成立；
综上所述：当△A'BC为等腰三角形时，AE的长为：或．
故答案为：或．
练习册系列答案
相关题目
