题目内容
现有代数式x+y,x-y,xy和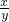 ,当x和y取哪些值时,能使其中的三个代数式的值相等?
,当x和y取哪些值时,能使其中的三个代数式的值相等?
解:当x= ,y=-1或x=-
,y=-1或x=- ,y=-1时,能使其中的三个代数式的值相等.理由如下:
,y=-1时,能使其中的三个代数式的值相等.理由如下:
首先必须y≠0,否则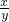 没有意义.
没有意义.
若x+y=x-y,则y=0,矛盾.所以x+y≠x-y.
若x=0,则由x+y=xy,或x-y=xy都得到y=0,
所以x≠0,即xy≠0.
因此三个相等的式子只有两种可能:
(1)x+y=xy=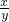 ,
,
由后一等式得到,y=1或y=-1,
而y=1是不可能的,因为此时由第一个等式得到x+1=x,即x=0;
当y=-1时,由第一个等式得到x-1=-x,即2x=1,
所以x= ;
;
(2)x-y=xy=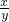 ,
,
由后一等式同样得到,y=1或y=-1,
同样y=1是不可能的,
而当y=-1时,由第一个等式得到2x=-1,
所以x=- .
.
分析:先讨论得到y≠0,则通过由x+y=xy,或x-y=xy都得到y=0,得到x≠0,即xy≠0;然后分类讨论:(1)x+y=xy=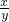 ,(2)x-y=xy=
,(2)x-y=xy=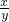 ,分别计算求出满足条件的x和y的值.
,分别计算求出满足条件的x和y的值.
点评:本题考查了利用代数式的值相等建立等量关系得到字母的值,也考查了分类讨论思想的运用.
 ,y=-1或x=-
,y=-1或x=- ,y=-1时,能使其中的三个代数式的值相等.理由如下:
,y=-1时,能使其中的三个代数式的值相等.理由如下:首先必须y≠0,否则
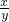 没有意义.
没有意义.若x+y=x-y,则y=0,矛盾.所以x+y≠x-y.
若x=0,则由x+y=xy,或x-y=xy都得到y=0,
所以x≠0,即xy≠0.
因此三个相等的式子只有两种可能:
(1)x+y=xy=
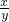 ,
,由后一等式得到,y=1或y=-1,
而y=1是不可能的,因为此时由第一个等式得到x+1=x,即x=0;
当y=-1时,由第一个等式得到x-1=-x,即2x=1,
所以x=
 ;
;(2)x-y=xy=
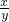 ,
,由后一等式同样得到,y=1或y=-1,
同样y=1是不可能的,
而当y=-1时,由第一个等式得到2x=-1,
所以x=-
 .
.分析:先讨论得到y≠0,则通过由x+y=xy,或x-y=xy都得到y=0,得到x≠0,即xy≠0;然后分类讨论:(1)x+y=xy=
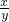 ,(2)x-y=xy=
,(2)x-y=xy=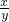 ,分别计算求出满足条件的x和y的值.
,分别计算求出满足条件的x和y的值.点评:本题考查了利用代数式的值相等建立等量关系得到字母的值,也考查了分类讨论思想的运用.

练习册系列答案
 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目