题目内容
已知sinα<cosα,那么锐角α的取值范围是( )A.30°<α<45°
B.0°<α<45°
C.45°<α<60°
D.0°<α<90°
【答案】分析:首先根据正余弦的转换方法,得:cosα=sin(90°-α),
又sinα<cosα,即sinα<sin(90°-α),
再根据正弦值随着角的增大而增大,进行分析.
解答:解:∵cosα=sin(90°-α),
∴sinα<cosα=sin(90°-α).
又正弦值随着角的增大而增大,
得α<90°-α,
∴α<45°.
又α是锐角,则α的取值范围是0°<α<45度.
故选B.
点评:掌握正余弦的转换方法,同时掌握锐角三角函数值的变化规律.
又sinα<cosα,即sinα<sin(90°-α),
再根据正弦值随着角的增大而增大,进行分析.
解答:解:∵cosα=sin(90°-α),
∴sinα<cosα=sin(90°-α).
又正弦值随着角的增大而增大,
得α<90°-α,
∴α<45°.
又α是锐角,则α的取值范围是0°<α<45度.
故选B.
点评:掌握正余弦的转换方法,同时掌握锐角三角函数值的变化规律.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
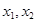 分别是一元二次方程
分别是一元二次方程
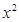 +
+
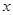 +
+ =0(
=0( =-
=- ,
,  =
=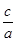
 ,
, 是方程
是方程 的值;
的值; )是关于x的方程2
)是关于x的方程2 的两个根,求角
的两个根,求角