题目内容
已知正数a,b满足a3b+ab3-2a2b+2ab2=7ab-8,则a2-b2=
- A.1
- B.3
- C.5
- D.不能确定
B
分析:首先将a3b+ab3-2a2b+2ab2=7ab-8通过提取公因式、运用完全平方式、添加项转化为ab(a-b-1)2+2(ab-2)2=0.再根据a、b均为正数以及非负数的性质,得到a-b=1、ab=2,进而解出a、b的值,代入a2-b2求得结果.
解答:∵a3b+ab3-2a2b+2ab2=7ab-8,
?ab(a2+b2)-2ab(a-b)=7ab-8,
?ab(a2-2ab+b2)-2ab(a-b)+2a2b2-7ab+8=0,
?ab(a-b)2-2ab(a-b)+2a2b2-7ab+8=0,
?ab[(a-b)2-2(a-b)+1]+2(a2b2-4ab+4)=0,
?ab(a-b-1)2+2(ab-2)2=0,
∵a、b均为正数,
∴ab>0,
∴a-b-1=0,ab-2=0,
即a-b=1,ab=2,
解方程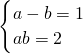 ,
,
解得a=2、b=1,a=-1、b=-2(不合题意,舍去),
∴a2-b2=4-1=3.
故选B.
点评:本题考查因式分解的应用、完全平方式、非负数的性质.解决本题的关键是将原式a3b+ab3-2a2b+2ab2=7ab-8转化为ab(a-b-1)2+2(ab-2)2=0形式,根据已知与非负数的性质确定出a、b的值.
分析:首先将a3b+ab3-2a2b+2ab2=7ab-8通过提取公因式、运用完全平方式、添加项转化为ab(a-b-1)2+2(ab-2)2=0.再根据a、b均为正数以及非负数的性质,得到a-b=1、ab=2,进而解出a、b的值,代入a2-b2求得结果.
解答:∵a3b+ab3-2a2b+2ab2=7ab-8,
?ab(a2+b2)-2ab(a-b)=7ab-8,
?ab(a2-2ab+b2)-2ab(a-b)+2a2b2-7ab+8=0,
?ab(a-b)2-2ab(a-b)+2a2b2-7ab+8=0,
?ab[(a-b)2-2(a-b)+1]+2(a2b2-4ab+4)=0,
?ab(a-b-1)2+2(ab-2)2=0,
∵a、b均为正数,
∴ab>0,
∴a-b-1=0,ab-2=0,
即a-b=1,ab=2,
解方程
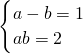 ,
,解得a=2、b=1,a=-1、b=-2(不合题意,舍去),
∴a2-b2=4-1=3.
故选B.
点评:本题考查因式分解的应用、完全平方式、非负数的性质.解决本题的关键是将原式a3b+ab3-2a2b+2ab2=7ab-8转化为ab(a-b-1)2+2(ab-2)2=0形式,根据已知与非负数的性质确定出a、b的值.

练习册系列答案
相关题目
已知正数a,b满足a3b+ab3-2a2b+2ab2=7ab-8,则a2-b2=( )
| A、1 | B、3 | C、5 | D、不能确定 |