题目内容
 如图,某校有一块长为(a+b)米,宽为b米的长方形场地(即空白的部分),学校计划把它的各边长都扩大b米,作为健身场地.
如图,某校有一块长为(a+b)米,宽为b米的长方形场地(即空白的部分),学校计划把它的各边长都扩大b米,作为健身场地.(1)用含a、b的代数式表示新长方形比原长方形扩大的面积(即阴影部分面积);
(2)求出当a=10米,b=3米时的阴影部分面积.
分析:(1)阴影部分的面积=大长方形面积-小长方形面积,表示出即可;
(2)将a与b代入计算即可求出值.
(2)将a与b代入计算即可求出值.
解答:解:(1)根据题意得:(a+b+b)(b+b)-(a+b)b=ab+3b2;
(2)当a=10,b=3时,ab+3b2=10×3+3×32=57.
(2)当a=10,b=3时,ab+3b2=10×3+3×32=57.
点评:此题考查了整式混合运算的应用,弄清题意是解本题的关键.

练习册系列答案
相关题目
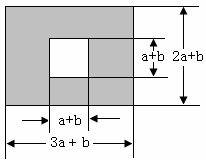
 如图,某校有一块长为(3a+b)米,宽为(2a+b)米的长方形地块,学校计划将阴影部分进行绿化,中间将修建一座雕像.
如图,某校有一块长为(3a+b)米,宽为(2a+b)米的长方形地块,学校计划将阴影部分进行绿化,中间将修建一座雕像.