题目内容
（2013•威海）如图，AC⊥CD，垂足为点C，BD⊥CD，垂足为点D，AB与CD交于点O．若AC=1，BD=2，CD=4，则AB=5
5
．分析：首先过点B作BE∥CD，交AC的延长线于点E，易证得四边形BDCE是矩形，然后由勾股定理求得答案．
解答：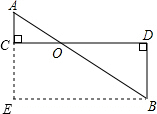
解：过点B作BE∥CD，交AC的延长线于点E，
∵AC⊥CD，BD⊥CD，
∴AC∥BD，∠D=90°，
∴四边形BDCE是平行四边形，
∴平行四边形BDCE是矩形，
∴CE=BD=2，BE=CD=4，∠E=90°，
∴AE=AC+CE=1+2=3，
∴在Rt△ABE中，AB=
=5．
故答案为：5．
解：过点B作BE∥CD，交AC的延长线于点E，∵AC⊥CD，BD⊥CD，
∴AC∥BD，∠D=90°，
∴四边形BDCE是平行四边形，
∴平行四边形BDCE是矩形，
∴CE=BD=2，BE=CD=4，∠E=90°，
∴AE=AC+CE=1+2=3，
∴在Rt△ABE中，AB=
| AE2+BE2 |
故答案为：5．
点评：此题考查了矩形的判定与性质以及勾股定理．此题难度不大，注意掌握辅助线的作法，注意掌握数形结合思想的应用．
练习册系列答案
相关题目
（2013•威海）如图，在△ABC中，∠ACB=90°，BC的垂直平分线EF交BC于点D，交AB于点E，且BE=BF，添加一个条件，仍不能证明四边形BECF为正方形的是（ ）
（2013•威海）如图，在△ABC中，∠A=36°，AB=AC，AB的垂直平分线OD交AB于点O，交AC于点D，连接BD，下列结论错误的是（ ）
（2013•威海）如图是由6个同样大小的正方体摆成的几何体．将正方体①移走后，所得几何体（ ）
（2013•威海）如图，在平面直角坐标系中，直线y=