题目内容
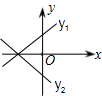
已知直线y1=k1x+b1，y2=k2x+b2，满足b1＜b2，且k1k2＜0，两直线的图象是
- A.
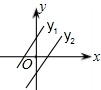
- B.
- C.
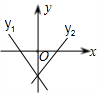
- D.
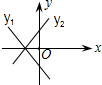
D
分析：由k1k2＜0，可知两条直线的增减性；再由b1＜b2，可知直线y1与y轴的交点在y2与y轴的交点的下边，而不是交于y轴上同一点．
解答：k1k2＜0，则k1与k2异号，
因而两个函数一个y随x的增大而增大，另一个y随x的增大而减小，因而A是错误的；
b1＜b2，则y1与y轴的交点在y2与y轴的交点的下边，因而B、C都是错误的．
故选D．
点评：函数值y随x的增大而减小?k＜0，函数值y随x的增大而增大?k＞0；
一次函数y=kx+b图象与y轴的正半轴相交?b＞0，一次函数y=kx+b图象与y轴的负半轴相交?b＜0，一次函数y=kx+b图象过原点?b=0．
分析：由k1k2＜0，可知两条直线的增减性；再由b1＜b2，可知直线y1与y轴的交点在y2与y轴的交点的下边，而不是交于y轴上同一点．
解答：k1k2＜0，则k1与k2异号，
因而两个函数一个y随x的增大而增大，另一个y随x的增大而减小，因而A是错误的；
b1＜b2，则y1与y轴的交点在y2与y轴的交点的下边，因而B、C都是错误的．
故选D．
点评：函数值y随x的增大而减小?k＜0，函数值y随x的增大而增大?k＞0；
一次函数y=kx+b图象与y轴的正半轴相交?b＞0，一次函数y=kx+b图象与y轴的负半轴相交?b＜0，一次函数y=kx+b图象过原点?b=0．
练习册系列答案
相关题目
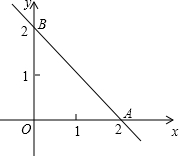如图，已知直线y1=k1x+b1分别与x轴，y轴交于点A、B，另一条直线y2=k2x+b2经过点C（0，1），且把△AOB分成面积相等的两部分，试分别确定两条直线的解析式．