Question

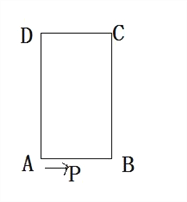
【题目】如图，长方形ABCD中，AB=4cm，BC=6cm，现有一动点P从A出发以2cm/秒的速度，沿矩形的边A—B—C—D回到点A，设点P的运动时间为t秒。

（1）当t=3秒时，求△ABP的面积；

（2）当t为何值时，点P与点A的距离为5cm？

（3）当t为何值时（2＜t＜5），以线段AD、CP、AP的长度为三角形是直角三角形，且AP是斜边。

Answer 1

【答案】(1)4cm2；（2）秒或秒；（3）秒.

【解析】试题分析：(1)、求出P运动的距离，得出O在BC上，根据三角形面积公式求出即可；(2)、分为三种情况：P在BC上，P在DC上，P在AD上，根据勾股定理得出关于t的方程，求出即可；(3)、求出BP=2t﹣4，CP=10﹣2t，根据AP2=AB2+BP2=42+（2t﹣4）2和AD2+CP2=AP2得出方程62+（10﹣2t）2=42+（2t﹣4）2，求出方程的解即可．

试题解析：(1)、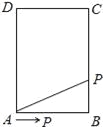

当t=3时，点P的路程为2×3=6cm， ∵AB=4cm，BC=6cm ∴点P在BC上， ∴（cm2）．

(2)、（Ⅰ）若点P在BC上，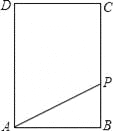

∵在Rt△ABP中，AP=5，AB=4 ∴BP=2t﹣4=3， ∴；

（Ⅱ）若点P在DC上，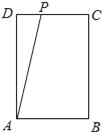

则在Rt△ADP中，AP是斜边， ∵AD=6， ∴AP＞6， ∴AP≠5；

（Ⅲ）若点P在AD上，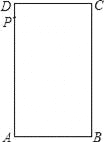

AP=5， 则点P的路程为20﹣5=15， ∴， 综上，当秒或时，AP=5cm．

(3)、当2＜t＜5时，点P在BC边上， ∵BP=2t﹣4，CP=10﹣2t， ∴AP2=AB2+BP2=42+（2t﹣4）2

由题意，有AD2+CP2=AP2 ∴62+（10﹣2t）2=42+（2t﹣4）2 ∴t=＜5， 即t=．