题目内容
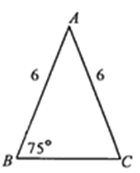
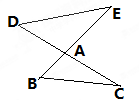
如果将一个三角形绕着它一个角的顶点旋转后使这个角的一边与另一边重叠,再将旋转后的三角形进行相似缩放,使重叠的两条边互相重合,我们称这样的图形变换为三角形转似,这个角的顶点称为转似中心,所得的三角形称为原三角形的转似三角形。如图,在△ABC中,AB=6,BC=7,AC=5,△ 是△ABC以点C为转似中心的其中一个转似三角形,那么以点C为转似中心的另一个转似三角形△
是△ABC以点C为转似中心的其中一个转似三角形,那么以点C为转似中心的另一个转似三角形△ (点
(点 分别与A、B对应)的边
分别与A、B对应)的边 的长为_____。
的长为_____。

 是△ABC以点C为转似中心的其中一个转似三角形,那么以点C为转似中心的另一个转似三角形△
是△ABC以点C为转似中心的其中一个转似三角形,那么以点C为转似中心的另一个转似三角形△ (点
(点 分别与A、B对应)的边
分别与A、B对应)的边 的长为_____。
的长为_____。
 .
.试题分析:先根据条件证明△ABC∽△A1B1C就可以求出A1C中,再证明△ABC∽△A2B2C就可以求出结论.
解:∵△ABC∽△A1B1C,

∴AC:A1C=BC:B1C.
∵AB=6,BC=7,AC=5,
∴5:A1C=7:5,
∴A1C=25:7.
∵△ABC∽△A2B2C,
∴BC:B2C=AB:A2B2,
∴
 =
= ,
,∴A2B2=
 .
.故答案为:
 .
.
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
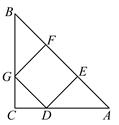

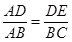 ,请添加一个条件,使
,请添加一个条件,使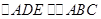 ,这个条件可以是______.
,这个条件可以是______.

 ,它的实际长度约为( )
,它的实际长度约为( ) ;
;
 b
b 如图所示,则下列4个三角形中,与△
如图所示,则下列4个三角形中,与△