题目内容
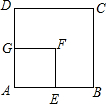
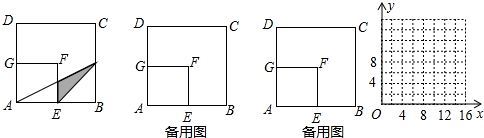
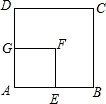
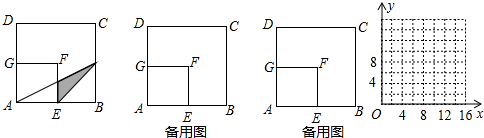
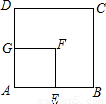
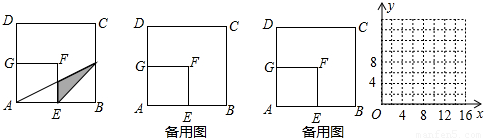
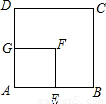
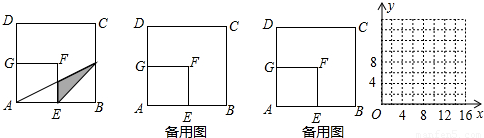
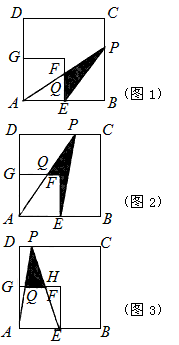
如图,在边长为8厘米的正方形ABCD内,贴上一个边长为4厘米的正方形AEFG,正方形ABCD未被盖住的部分为多边形EBCDGF,动点P从点B出发,沿B→C→D方向以1厘米/秒速度运动,到点D停止,连接PA,PE,设点P运动x秒后,△APE与多边形EBCDGF重叠部分的面积为y厘米2。
(1)当x=5时,求y的值;
(2)当x=10时,求y的值;
(3)求y与x之间的函数关系式;
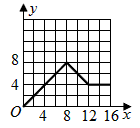
(4)在给出的直角坐标系中画出y与x之间的函数图象。
(1)当x=5时,求y的值;
(2)当x=10时,求y的值;
(3)求y与x之间的函数关系式;
(4)在给出的直角坐标系中画出y与x之间的函数图象。
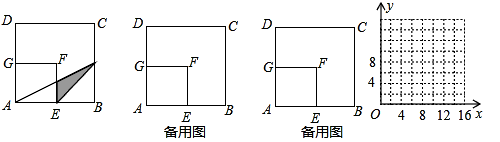
| 解:设AP与EF(或GF)交于点Q, (1)在正方形ABCD和正方形AEFG中,E为AB中点, ∴EQ∥BP,即EQ为△ABP的中位线, 当x=5时,PB=5, ∴QE=  PB= PB= , ,∵BE=4, ∴y= 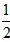 EQ·EB= EQ·EB=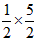 ×4=5; ×4=5;(2)当x=10时,如图2,PD=6,GQ=3, QF=FG-GQ=1,AE=4, ∴ 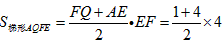 =10, =10,S△PAE=  AE·BC= AE·BC= ×4×8=16, ×4×8=16,∴y=S△PAE-S梯形AQFE=16-10=6; (3)当0≤x≤8时,y=x; 当8≤x≤12时,y=-x+16; 当12≤x≤16时,y=4; (4)图象如下: |
  |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目