题目内容
若我们把边长与面积都是整数的三角形称作整数三角形,那么边长为3,4,5的三角形由于其面积为6因此为整数三角形.小明在研究时发现,直角三角形中存在大量的整数三角形,但他没有发现锐角三角形中的整数三角形以及钝角三角形中的整数三角形.你认为存在吗?若你认为存在的话,请分别画出一个锐角整数三角形和一个钝角整数三角形(画出计算面积所需的高,在图上标出相关数据.且其中至少有一个为不等边三角形);若你认为不存在,请简单的说一下理由.
解:存在,
如边长为5,5,6(边长为6的边为底,高为4);
5,5,8(边长为8的边为底,高为3);
10,10,12(边长为12的边为底,高为8);
15,13,4(边长为14的边为底,高为12);

分析:根据勾股定理计算即可.
点评:此题主要考查了勾股定理的应用,根据已知熟练利用勾股定理求出勾股数是解题关键.

如边长为5,5,6(边长为6的边为底,高为4);
5,5,8(边长为8的边为底,高为3);
10,10,12(边长为12的边为底,高为8);
15,13,4(边长为14的边为底,高为12);

分析:根据勾股定理计算即可.
点评:此题主要考查了勾股定理的应用,根据已知熟练利用勾股定理求出勾股数是解题关键.

练习册系列答案
相关题目
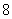 ,∠A=60°,E为
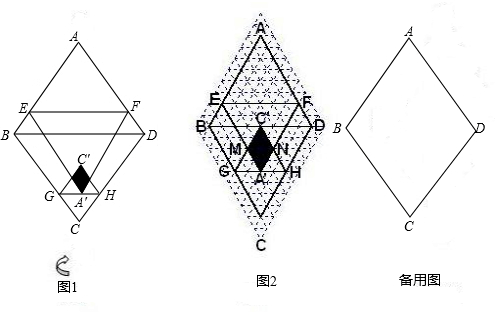
,∠A=60°,E为 边上的点,过点E作EF∥BD交AD于点F.将菱形先沿EF按图1所示方式折叠,点A落在点
边上的点,过点E作EF∥BD交AD于点F.将菱形先沿EF按图1所示方式折叠,点A落在点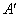 处,过点
处,过点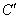 处,
处,
 与
与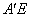 与
与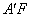 于点M、N.若点
于点M、N.若点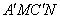 (即图中阴影部分)为“重叠四边形”.
(即图中阴影部分)为“重叠四边形”.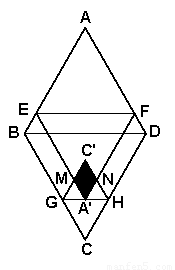

 ,若重叠四边形
,若重叠四边形