题目内容
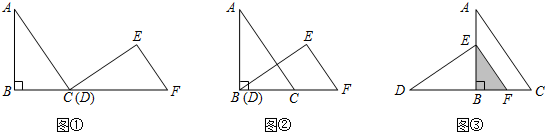
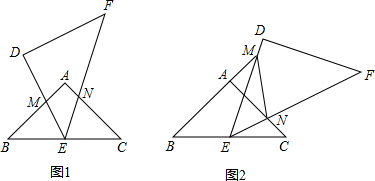
△ABC和△DEF是两个形状、大小完全相同的直角三角形，如图①所示，三条边BC、AB、AC的长分别是6cm、8cm、10cm，且B、C、D、F在同一条直线上．
（1）如果△ABC朝着某个方向平移后得如图②所示，则△ABC平移的方向是什么？平移的距离是多少？
（2）△ABC平移至图③所示的位置，如果BD=6.4cm，则△EBF的面积是多少？
解：（1）由图可知，△ABC平移的方向沿BC方向，
∵BC=6cm，
∴平移距离是6cm；
（2）∵BD=6.4cm，DF=AC=10cm，
∴BF=DF-BD=10-6.4=3.6cm，
∵∠BFE=∠EFD，∠EBF=∠DEF=90°，
∴△EBF∽△DEF，
∴
=
，
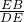即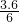
=
，
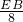解得EB=4.8cm，
∴△EBF的面积=
BF•EB=×3.6×4.8=8.64cm2．
分析：（1）根据平移的性质结合图形即可确定平移方向为沿BC方向，对应点D之间的距离为平移距离；
（2）先求出BF的长度，再利用△EBF和△DEF相似，根据相似三角形对应边成比例列式求出EB的长度，然后根据三角形的面积公式列式进行计算即可得解．
点评：本题考查了平移的性质，相似三角形的判定与性质，（2）利用相似三角形求出EB的长度是解题的关键．
∵BC=6cm，
∴平移距离是6cm；
（2）∵BD=6.4cm，DF=AC=10cm，
∴BF=DF-BD=10-6.4=3.6cm，
∵∠BFE=∠EFD，∠EBF=∠DEF=90°，
∴△EBF∽△DEF，
∴
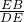=，即
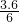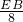=，解得EB=4.8cm，
∴△EBF的面积=
BF•EB=×3.6×4.8=8.64cm2．分析：（1）根据平移的性质结合图形即可确定平移方向为沿BC方向，对应点D之间的距离为平移距离；
（2）先求出BF的长度，再利用△EBF和△DEF相似，根据相似三角形对应边成比例列式求出EB的长度，然后根据三角形的面积公式列式进行计算即可得解．
点评：本题考查了平移的性质，相似三角形的判定与性质，（2）利用相似三角形求出EB的长度是解题的关键．
练习册系列答案
全能练考卷系列答案
相关题目
24、如图，三角形ABC和DEF是两个形状大小完全相同的等腰直角三角形，∠B=∠DEF=90°，点B，C，E，F在同一直线上，现从点C，E重合的位置出发，让三角形ABC在直线EF上向右作匀速运动，而DEF的位置不动，设两个三角形重合部分的面积为y，运动的距离为x，下面表示y与x的函数关系的图象大致是（ ）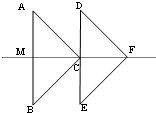
如图，△ABC和△DEF是两个形状大小完全相同的等腰直角三角形，∠ACB=∠DFE=90°，点C落在DE的中点处，且AB的中点M与C、F三点共线，现在让△ABC在直线MF上向右作匀速移动，而△DEF不动，设两个三角形重合部分的面积为y，向右水平移动的距离为x，则y与x的函数关系的图象大致是（ ）