ΧβΡΩΡΎ»ί
Θ®2004•ΙΰΕϊ±θΘ©“―÷ΣΘΚ≈ΉΈοœΏy=-x2-Θ®m+3Θ©x+m2-12”κx÷αΫΜ”ΎAΘ®x1Θ§0Θ©ΓΔBΘ®x2Θ§0Θ©ΝΫΒψΘ§«“x1ΘΦ0Θ§x2ΘΨ0Θ§≈ΉΈοœΏ”κy÷αΫΜ”ΎΒψCΘ§OB=2OAΘ°Θ®1Θ©«σ≈ΉΈοœΏΒΡΫβΈω ΫΘΜ
Θ®2Θ©‘Ύx÷α…œΘ§ΒψAΒΡΉσ≤ύΘ§«σ“ΜΒψEΘ§ ΙΓςECO”κΓςCAOœύΥΤΘ§≤ΔΥΒΟς÷±œΏECΨ≠ΙΐΘ®1Θ©÷–≈ΉΈοœΏΒΡΕΞΒψDΘΜ
Θ®3Θ©ΙΐΘ®2Θ©÷–ΒΡΒψEΒΡ÷±œΏy=
 x+b”κΘ®1Θ©÷–ΒΡ≈ΉΈοœΏœύΫΜ”ΎMΓΔNΝΫΒψΘ§Ζ÷±πΙΐMΓΔNΉςx÷αΒΡ¥ΙœΏΘ§¥ΙΉψΈΣMΓδΓΔNΓδΘ§ΒψPΈΣœΏΕΈMN…œ“ΜΒψΘ§ΒψPΒΡΚαΉχ±ξΈΣtΘ§ΙΐΒψPΉςΤΫ––”Ύy÷αΒΡ÷±œΏΫΜΘ®1Θ©÷–Υυ«σ≈ΉΈοœΏ”ΎΒψQΘ° «Ζώ¥φ‘Ύt÷ΒΘ§ ΙSΧί–ΈMM'N'NΘΚSΓςQMN=35ΘΚ12ΘΩ»τ¥φ‘ΎΘ§«σ≥ω¬ζΉψΧθΦΰΒΡt÷ΒΘΜ»τ≤Μ¥φ‘ΎΘ§«κΥΒΟςάμ”…Θ°
x+b”κΘ®1Θ©÷–ΒΡ≈ΉΈοœΏœύΫΜ”ΎMΓΔNΝΫΒψΘ§Ζ÷±πΙΐMΓΔNΉςx÷αΒΡ¥ΙœΏΘ§¥ΙΉψΈΣMΓδΓΔNΓδΘ§ΒψPΈΣœΏΕΈMN…œ“ΜΒψΘ§ΒψPΒΡΚαΉχ±ξΈΣtΘ§ΙΐΒψPΉςΤΫ––”Ύy÷αΒΡ÷±œΏΫΜΘ®1Θ©÷–Υυ«σ≈ΉΈοœΏ”ΎΒψQΘ° «Ζώ¥φ‘Ύt÷ΒΘ§ ΙSΧί–ΈMM'N'NΘΚSΓςQMN=35ΘΚ12ΘΩ»τ¥φ‘ΎΘ§«σ≥ω¬ζΉψΧθΦΰΒΡt÷ΒΘΜ»τ≤Μ¥φ‘ΎΘ§«κΥΒΟςάμ”…Θ°
ΓΨ¥πΑΗΓΩΖ÷ΈωΘΚΘ®1Θ©Ω……η≥ωAΓΔBΒΡΉχ±ξΘ§»ΜΚσ”ΟΈΛ¥οΕ®άμ±μ Ψ≥ωΝΫΒψΚαΉχ±ξΒΡΚΆ”κΜΐΘ§»ΜΚσΗυΨίOB=2OAΘ§Φ¥BΒψΒΡΚαΉχ±ξΈΣAΒψΚαΉχ±ξΒΡ2±ΕΝΣΝΔ»ΐ ΫΩ…ΒΟ≥ωmΒΡ÷ΒΘ°Φ¥Ω…«σ≥ω≈ΉΈοœΏΒΡΫβΈω ΫΘΜ
Θ®2Θ©ΗυΨίΓςECO”κΓςCAOœύΥΤΘ§Ω…Ά®ΙΐœύΥΤ»ΐΫ«–ΈΒΡΕ‘”Π±Ώ≥…±»άΐœΏΕΈ«σ≥ωOEΒΡ≥ΛΘ§Φ¥Ω…ΒΟ≥ωEΒψΒΡΉχ±ξΘ§ΫχΕχΩ…«σ≥ωΙΐEΒψ÷±œΏΒΡΫβΈω ΫΘ§»ΜΚσΫΪ≈ΉΈοœΏΕΞΒψ¥ζ»κ÷±œΏΒΡΫβΈω Ϋ÷–Ϋχ––≈–ΕœΦ¥Ω…ΘΜ
Θ®3Θ©ΙΐMΓΔNΖ÷±πΉς÷±œΏPQΒΡ¥ΙœΏΚσΩ…ΖΔœ÷Θ§»ΐΫ«–ΈQMNΩ…“‘“‘QPΈΣΒΉΘ§“‘MΓΔNΝΫΒψΒΡΚαΉχ±ξ≤νΈΣΗΏά¥«σΒΟΤδΟφΜΐΘ§ΕχΧί–ΈΒΡΟφΜΐΩ…“‘“‘MΓΔNΝΫΒψΒΡΉίΉχ±ξΒΡΚΆ”κΝΫΒψΚαΉχ±ξΒΡ≤νΈΣΗΏά¥«σΘ§“ρ¥Υ»ΐΫ«–ΈQMNΚΆΧί–ΈΒΡΟφΜΐ±» ΒΦ «QMΚΆMΓΔNΝΫΒψΒΡΉίΉχ±ξΒΡ±»Θ°Ω…ΝΣΝΔ÷±œΏMN”κ≈ΉΈοœΏΒΡΫβΈω Ϋ«σ≥ωMΓΔNΝΫΒψΉίΉχ±ξΒΡΚΆΘ§»ΜΚσΫΪt¥ζ»κ≈ΉΈοœΏΚΆ÷±œΏMNΒΡΫβΈω Ϋ÷–«σ≥ωQPΒΡ±μ¥ο ΫΘ§ΗυΨίΧβ÷–Ηχ≥ωΒΡΝΫΗωΆΦ–ΈΒΡΟφΜΐ±»Φ¥Ω…«σΒΟtΒΡ÷ΒΘ°
Ϋβ¥πΘΚ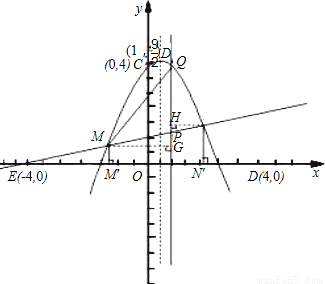 ΫβΘΚΘ®1Θ©ΓΏx1ΘΦ0Θ§x2ΘΨ0Θ°
ΫβΘΚΘ®1Θ©ΓΏx1ΘΦ0Θ§x2ΘΨ0Θ°
ΓύOA=x1Θ§OB=x2
ΓΏx1Θ§x2 «ΖΫ≥Χ-x2-Θ®m+3Θ©x+m2-12=0ΒΡΝΫΗω Β ΐΗυ
Γύx1+x2=-2Θ®m+3Θ©ΔΌΘ§x1•x2=-2Θ®m2-12Θ©ΔΎx2=-2x1Δέ
ΝΣΝΔΔΌΘ§ΔΎΘ§Δέ’ϊάμΒΟΘΚm2+8m+16=0Θ§
ΫβΒΟm=-4Θ°
Γύ≈ΉΈοœΏΒΡΫβΈω ΫΈΣy=-x2+x+4ΘΜ
Θ®2Θ©…ηΒψEΘ®xΘ§0Θ©Θ§‘ρOE=-xΘ°
ΓΏΓςECO”κΓςCAOœύΥΤΘ§
Γύ Θ§
Θ§ Θ§x=-8
Θ§x=-8
ΓύΒψEΘ®-8Θ§0Θ©
…ηΙΐEΓΔCΝΫΒψΒΡ÷±œΏΫβΈω ΫΈΣy=kΓδx+bΓδΘ§
‘ρ”–ΘΚ Θ§
Θ§
ΫβΒΟ
Γύ÷±œΏECΒΡΫβΈω ΫΈΣy= x+4Θ°
x+4Θ°
ΓΏ≈ΉΈοœΏΒΡΕΞΒψDΘ®1Θ§ Θ©Θ§Β±x=1 ±Θ§y=
Θ©Θ§Β±x=1 ±Θ§y=
ΓύΒψD‘Ύ÷±œΏEC…œΘΜ
Θ®3Θ©¥φ‘Ύt÷ΒΘ§ ΙSΧί–ΈMM'N'NΘΚSΓςQMN=35ΘΚ12Θ°
ΓΏEΘ®-8Θ§0Θ©Θ§
Γύ ×Θ®-8Θ©+b=0Θ§
×Θ®-8Θ©+b=0Θ§
Γύb=2Θ§y= x+2Θ°
x+2Θ°
Γύx=4Θ®y-2Θ©Θ°
Γύy=- [4Θ®y-2Θ©2+4Θ®y-2Θ©+4]Θ§
[4Θ®y-2Θ©2+4Θ®y-2Θ©+4]Θ§
’ϊάμΒΟ8y2-35y+6=0Θ§
…ηMΘ®xmΘ§ymΘ©Θ°
ΓύMMΓδ=ymΘ§NNΓδ=ynΘ§
ΓύymΘ§yn «ΖΫ≥Χ8y2-35y+6=0ΒΡΝΫΗω Β ΐΗυΘ§ym+yn=
ΓύSΧί–Έ= Θ®ym+ynΘ©Θ®xn-xmΘ©
Θ®ym+ynΘ©Θ®xn-xmΘ©
ΓΏΒψP‘Ύ÷±œΏy= x+2…œΘ§ΒψQ‘ΎΘ®1Θ©÷–≈ΉΈοœΏ…œΘ§
x+2…œΘ§ΒψQ‘ΎΘ®1Θ©÷–≈ΉΈοœΏ…œΘ§
ΓύΒψPΘ®tΘ§ t+2Θ©ΓΔΒψQΘ®tΘ§-
t+2Θ©ΓΔΒψQΘ®tΘ§- t2+t+4Θ©
t2+t+4Θ©
ΓύPQ=- t2+t+4-
t2+t+4- t-2=-
t-2=- t2-
t2- t+2Θ§
t+2Θ§
Ζ÷±πΙΐMΓΔNΉς÷±œΏPQΒΡ¥ΙœΏΘ§¥ΙΉψΈΣGΓΔHΘ§‘ρGM=t-xmΘ§NH=xn-t
ΓύSΓςQMN=SΓςQMP+SΓςQNP= PQΘ®xn-xmΘ©
PQΘ®xn-xmΘ©
ΓΏSΧί–ΈMM'N'NΘΚSΓςQMN=35ΘΚ12Θ§
Γύ =
= Θ§
Θ§
’ϊάμΒΟΘΚ2t2-3t-2=0Θ§
ΫβΒΟt=- Θ§t=2Θ°
Θ§t=2Θ°
“ρ¥ΥΒ±t=- Μρt=2 ±Θ§SΧί–ΈMM'N'NΘΚSΓςQMN=35ΘΚ12Θ°
Μρt=2 ±Θ§SΧί–ΈMM'N'NΘΚSΓςQMN=35ΘΚ12Θ°
ΒψΤάΘΚ±ΨΧβΈΣΕΰ¥ΈΚ· ΐΉέΚœΧβΘ§ΩΦ≤ιΝΥΕΰ¥ΈΚ· ΐΫβΈω ΫΒΡ»ΖΕ®ΓΔΆΦ–ΈΟφΜΐΒΡ«σΖ®ΓΔΚ· ΐΆΦœσΫΜΒψΒ»÷Σ ΕΒψΘ§Ρ―Ε»Ϋœ¥σΘ°
Θ®2Θ©ΗυΨίΓςECO”κΓςCAOœύΥΤΘ§Ω…Ά®ΙΐœύΥΤ»ΐΫ«–ΈΒΡΕ‘”Π±Ώ≥…±»άΐœΏΕΈ«σ≥ωOEΒΡ≥ΛΘ§Φ¥Ω…ΒΟ≥ωEΒψΒΡΉχ±ξΘ§ΫχΕχΩ…«σ≥ωΙΐEΒψ÷±œΏΒΡΫβΈω ΫΘ§»ΜΚσΫΪ≈ΉΈοœΏΕΞΒψ¥ζ»κ÷±œΏΒΡΫβΈω Ϋ÷–Ϋχ––≈–ΕœΦ¥Ω…ΘΜ
Θ®3Θ©ΙΐMΓΔNΖ÷±πΉς÷±œΏPQΒΡ¥ΙœΏΚσΩ…ΖΔœ÷Θ§»ΐΫ«–ΈQMNΩ…“‘“‘QPΈΣΒΉΘ§“‘MΓΔNΝΫΒψΒΡΚαΉχ±ξ≤νΈΣΗΏά¥«σΒΟΤδΟφΜΐΘ§ΕχΧί–ΈΒΡΟφΜΐΩ…“‘“‘MΓΔNΝΫΒψΒΡΉίΉχ±ξΒΡΚΆ”κΝΫΒψΚαΉχ±ξΒΡ≤νΈΣΗΏά¥«σΘ§“ρ¥Υ»ΐΫ«–ΈQMNΚΆΧί–ΈΒΡΟφΜΐ±» ΒΦ «QMΚΆMΓΔNΝΫΒψΒΡΉίΉχ±ξΒΡ±»Θ°Ω…ΝΣΝΔ÷±œΏMN”κ≈ΉΈοœΏΒΡΫβΈω Ϋ«σ≥ωMΓΔNΝΫΒψΉίΉχ±ξΒΡΚΆΘ§»ΜΚσΫΪt¥ζ»κ≈ΉΈοœΏΚΆ÷±œΏMNΒΡΫβΈω Ϋ÷–«σ≥ωQPΒΡ±μ¥ο ΫΘ§ΗυΨίΧβ÷–Ηχ≥ωΒΡΝΫΗωΆΦ–ΈΒΡΟφΜΐ±»Φ¥Ω…«σΒΟtΒΡ÷ΒΘ°
Ϋβ¥πΘΚ
 ΫβΘΚΘ®1Θ©ΓΏx1ΘΦ0Θ§x2ΘΨ0Θ°
ΫβΘΚΘ®1Θ©ΓΏx1ΘΦ0Θ§x2ΘΨ0Θ°ΓύOA=x1Θ§OB=x2
ΓΏx1Θ§x2 «ΖΫ≥Χ-x2-Θ®m+3Θ©x+m2-12=0ΒΡΝΫΗω Β ΐΗυ
Γύx1+x2=-2Θ®m+3Θ©ΔΌΘ§x1•x2=-2Θ®m2-12Θ©ΔΎx2=-2x1Δέ
ΝΣΝΔΔΌΘ§ΔΎΘ§Δέ’ϊάμΒΟΘΚm2+8m+16=0Θ§
ΫβΒΟm=-4Θ°
Γύ≈ΉΈοœΏΒΡΫβΈω ΫΈΣy=-x2+x+4ΘΜ
Θ®2Θ©…ηΒψEΘ®xΘ§0Θ©Θ§‘ρOE=-xΘ°
ΓΏΓςECO”κΓςCAOœύΥΤΘ§
Γύ
 Θ§
Θ§ Θ§x=-8
Θ§x=-8ΓύΒψEΘ®-8Θ§0Θ©
…ηΙΐEΓΔCΝΫΒψΒΡ÷±œΏΫβΈω ΫΈΣy=kΓδx+bΓδΘ§
‘ρ”–ΘΚ
 Θ§
Θ§ΫβΒΟ

Γύ÷±œΏECΒΡΫβΈω ΫΈΣy=
 x+4Θ°
x+4Θ°ΓΏ≈ΉΈοœΏΒΡΕΞΒψDΘ®1Θ§
 Θ©Θ§Β±x=1 ±Θ§y=
Θ©Θ§Β±x=1 ±Θ§y=
ΓύΒψD‘Ύ÷±œΏEC…œΘΜ
Θ®3Θ©¥φ‘Ύt÷ΒΘ§ ΙSΧί–ΈMM'N'NΘΚSΓςQMN=35ΘΚ12Θ°
ΓΏEΘ®-8Θ§0Θ©Θ§
Γύ
 ×Θ®-8Θ©+b=0Θ§
×Θ®-8Θ©+b=0Θ§Γύb=2Θ§y=
 x+2Θ°
x+2Θ°Γύx=4Θ®y-2Θ©Θ°
Γύy=-
 [4Θ®y-2Θ©2+4Θ®y-2Θ©+4]Θ§
[4Θ®y-2Θ©2+4Θ®y-2Θ©+4]Θ§’ϊάμΒΟ8y2-35y+6=0Θ§
…ηMΘ®xmΘ§ymΘ©Θ°
ΓύMMΓδ=ymΘ§NNΓδ=ynΘ§
ΓύymΘ§yn «ΖΫ≥Χ8y2-35y+6=0ΒΡΝΫΗω Β ΐΗυΘ§ym+yn=

ΓύSΧί–Έ=
 Θ®ym+ynΘ©Θ®xn-xmΘ©
Θ®ym+ynΘ©Θ®xn-xmΘ©ΓΏΒψP‘Ύ÷±œΏy=
 x+2…œΘ§ΒψQ‘ΎΘ®1Θ©÷–≈ΉΈοœΏ…œΘ§
x+2…œΘ§ΒψQ‘ΎΘ®1Θ©÷–≈ΉΈοœΏ…œΘ§ΓύΒψPΘ®tΘ§
 t+2Θ©ΓΔΒψQΘ®tΘ§-
t+2Θ©ΓΔΒψQΘ®tΘ§- t2+t+4Θ©
t2+t+4Θ©ΓύPQ=-
 t2+t+4-
t2+t+4- t-2=-
t-2=- t2-
t2- t+2Θ§
t+2Θ§Ζ÷±πΙΐMΓΔNΉς÷±œΏPQΒΡ¥ΙœΏΘ§¥ΙΉψΈΣGΓΔHΘ§‘ρGM=t-xmΘ§NH=xn-t
ΓύSΓςQMN=SΓςQMP+SΓςQNP=
 PQΘ®xn-xmΘ©
PQΘ®xn-xmΘ©ΓΏSΧί–ΈMM'N'NΘΚSΓςQMN=35ΘΚ12Θ§
Γύ
 =
= Θ§
Θ§’ϊάμΒΟΘΚ2t2-3t-2=0Θ§
ΫβΒΟt=-
 Θ§t=2Θ°
Θ§t=2Θ°“ρ¥ΥΒ±t=-
 Μρt=2 ±Θ§SΧί–ΈMM'N'NΘΚSΓςQMN=35ΘΚ12Θ°
Μρt=2 ±Θ§SΧί–ΈMM'N'NΘΚSΓςQMN=35ΘΚ12Θ°ΒψΤάΘΚ±ΨΧβΈΣΕΰ¥ΈΚ· ΐΉέΚœΧβΘ§ΩΦ≤ιΝΥΕΰ¥ΈΚ· ΐΫβΈω ΫΒΡ»ΖΕ®ΓΔΆΦ–ΈΟφΜΐΒΡ«σΖ®ΓΔΚ· ΐΆΦœσΫΜΒψΒ»÷Σ ΕΒψΘ§Ρ―Ε»Ϋœ¥σΘ°

ΝΖœΑ≤αœΒΝ–¥πΑΗ
œύΙΊΧβΡΩ
 Θ®2004•ΙΰΕϊ±θΘ©–ΓΟςΆ§―ßΤοΉ‘––≥Β»ΞΫΦΆβ¥Κ”ΈΘ§œ¬ΆΦ±μ ΨΥϊάκΦ“ΒΡΨύάκyΘ®«ßΟΉΘ©”κΥυ”ΟΒΡ ±ΦδxΘ®–Γ ±Θ©÷°ΦδΙΊœΒΒΡΚ· ΐΆΦœσΘ°
Θ®2004•ΙΰΕϊ±θΘ©–ΓΟςΆ§―ßΤοΉ‘––≥Β»ΞΫΦΆβ¥Κ”ΈΘ§œ¬ΆΦ±μ ΨΥϊάκΦ“ΒΡΨύάκyΘ®«ßΟΉΘ©”κΥυ”ΟΒΡ ±ΦδxΘ®–Γ ±Θ©÷°ΦδΙΊœΒΒΡΚ· ΐΆΦœσΘ° x+b”κΘ®1Θ©÷–ΒΡ≈ΉΈοœΏœύΫΜ”ΎMΓΔNΝΫΒψΘ§Ζ÷±πΙΐMΓΔNΉςx÷αΒΡ¥ΙœΏΘ§¥ΙΉψΈΣMΓδΓΔNΓδΘ§ΒψPΈΣœΏΕΈMN…œ“ΜΒψΘ§ΒψPΒΡΚαΉχ±ξΈΣtΘ§ΙΐΒψPΉςΤΫ––”Ύy÷αΒΡ÷±œΏΫΜΘ®1Θ©÷–Υυ«σ≈ΉΈοœΏ”ΎΒψQΘ° «Ζώ¥φ‘Ύt÷ΒΘ§ ΙSΧί–ΈMM'N'NΘΚSΓςQMN=35ΘΚ12ΘΩ»τ¥φ‘ΎΘ§«σ≥ω¬ζΉψΧθΦΰΒΡt÷ΒΘΜ»τ≤Μ¥φ‘ΎΘ§«κΥΒΟςάμ”…Θ°
x+b”κΘ®1Θ©÷–ΒΡ≈ΉΈοœΏœύΫΜ”ΎMΓΔNΝΫΒψΘ§Ζ÷±πΙΐMΓΔNΉςx÷αΒΡ¥ΙœΏΘ§¥ΙΉψΈΣMΓδΓΔNΓδΘ§ΒψPΈΣœΏΕΈMN…œ“ΜΒψΘ§ΒψPΒΡΚαΉχ±ξΈΣtΘ§ΙΐΒψPΉςΤΫ––”Ύy÷αΒΡ÷±œΏΫΜΘ®1Θ©÷–Υυ«σ≈ΉΈοœΏ”ΎΒψQΘ° «Ζώ¥φ‘Ύt÷ΒΘ§ ΙSΧί–ΈMM'N'NΘΚSΓςQMN=35ΘΚ12ΘΩ»τ¥φ‘ΎΘ§«σ≥ω¬ζΉψΧθΦΰΒΡt÷ΒΘΜ»τ≤Μ¥φ‘ΎΘ§«κΥΒΟςάμ”…Θ°
 Θ®2004•ΙΰΕϊ±θΘ©–ΓΟςΆ§―ßΤοΉ‘––≥Β»ΞΫΦΆβ¥Κ”ΈΘ§œ¬ΆΦ±μ ΨΥϊάκΦ“ΒΡΨύάκyΘ®«ßΟΉΘ©”κΥυ”ΟΒΡ ±ΦδxΘ®–Γ ±Θ©÷°ΦδΙΊœΒΒΡΚ· ΐΆΦœσΘ°
Θ®2004•ΙΰΕϊ±θΘ©–ΓΟςΆ§―ßΤοΉ‘––≥Β»ΞΫΦΆβ¥Κ”ΈΘ§œ¬ΆΦ±μ ΨΥϊάκΦ“ΒΡΨύάκyΘ®«ßΟΉΘ©”κΥυ”ΟΒΡ ±ΦδxΘ®–Γ ±Θ©÷°ΦδΙΊœΒΒΡΚ· ΐΆΦœσΘ°