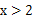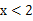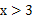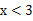题目内容
如图,已知抛物线y1=-2x2+2,直线y2=2x+2,当x任取一值时,x对应的函数值分别为y1、y2.若y1≠y2,取y1、y2中的较小值记为M;若y1=y2,记M=y1=y2,例如:当x=1时,y1=0,y2=4,y1<y2,此时M=0.下列判断: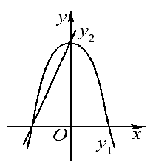
①当x>0时,y1>y2;
②当x<0时,x值越大,M值越小;
③使得M大于2的x值不存在;
④使得M=1的x值是-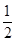 或
或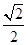 .
.
其中正确的是
| A.①② | B.①④ | C.②③ | D.③④ |
D.
解析试题分析:联立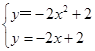 ,解得
,解得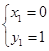 ,
,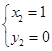 ,
,
所以,两交点坐标为(0,1),(1,0),
∴0<x<1时,y1>y2,
x>1时,y1<y2,故①错误;
∵y1≠y2,取y1,y2中的较小值记为M1,
∴x<0时,M=y1,y随x的增大而增大,
∴x值越大,M值越大,故②错误;
∵交点的纵坐标最大值为1,
∴M≤1,
∴使得M大于1的x值不存在,故③正确;
令y=1,则-2x2+2=1,2x+2=1
又∵(1,0)为两函数的交点坐标,解得x1=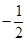 ,x2=
,x2=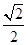 ,
,
∴使得M=1的x值是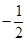 或
或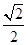 ,故④正确;
,故④正确;
综上所述,正确的是③④.
故选D.
考点: 1.二次函数的性质;2.一次函数的性质.

练习册系列答案
相关题目
反比例函数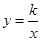 与一次函数
与一次函数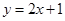 的图像的一个交点是(1,k),则
的图像的一个交点是(1,k),则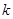 的值为( )
的值为( )
| A.﹣2 | B.2 | C.﹣3 | D.3 |
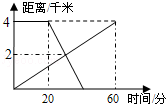
一辆汽车和一辆摩托车分别从 两地去同一城市,它们离
两地去同一城市,它们离 地的路程随时间变化的图像如图所示,则下列结论错误的是( )
地的路程随时间变化的图像如图所示,则下列结论错误的是( ) 
A.摩托车比汽车晚到 |
B. 两地的路程为 两地的路程为 |
C.摩托车的速度为 |
D.汽车的速度为 |
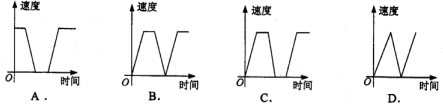
甲、乙两人在直线跑道上同起点、同终点、同方向匀速跑步500米,先到终点的人原地休息,已知甲先出发2秒,在跑步过程中,甲、乙两人的距离y(米)与乙出发的时间t(秒)之间的关系如图所示,给出以下结论:①a=8;②b=92;③c=123.其中正确的是 ( )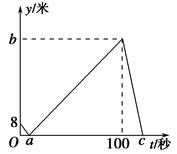
| A.①②③ | B.仅有①② |
| C.仅有①③ | D.仅有②③ |
一次函数y=-2x+4的图象与y轴的交点坐标是( )
| A.(0,4) | B.(4,0) |
| C.(2,0) | D.(0,2) |
已知正比例函数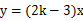 的图象过点(
的图象过点(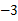 ,5),则
,5),则 的值为 ( )
的值为 ( )
A.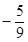 | B.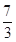 | C.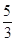 | D.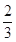 |
 轴于(2,0),交
轴于(2,0),交 轴于(0,3),当函数值大于0时,
轴于(0,3),当函数值大于0时,