题目内容
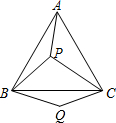（2012•仪陇县模拟）如图，P是等边三角形ABC内的一点，连接PA，PB，PC，以BP为边作∠PBQ=60°，且BQ=BP，连接CQ．观察并猜想AP与CQ之间的大小关系，并证明你的结论．分析：先猜想AP=CQ，再在△ABP与△CBQ中，由AB=CB，BP=BQ，∠ABC=∠PBQ=60°可得出∠ABP=∠CBQ，进而可判断出△ABP≌△CBQ，由全等三角形的对应边相等即可得出结论．
解答：猜想：AP=CQ
证明：在△ABP与△CBQ中，
∵AB=CB，BP=BQ，∠ABC=∠PBQ=60°，
∴∠ABP=∠ABC-∠PBC=∠PBQ-∠PBC=∠CBQ，
∴△ABP≌△CBQ，
∴AP=CQ
证明：在△ABP与△CBQ中，
∵AB=CB，BP=BQ，∠ABC=∠PBQ=60°，
∴∠ABP=∠ABC-∠PBC=∠PBQ-∠PBC=∠CBQ，
∴△ABP≌△CBQ，
∴AP=CQ
点评：本题考查的是等边三角形的性质及全等三角形的判定与性质，根据题意判断出△ABP≌△CBQ是解答此题的关键．
练习册系列答案
综合自测系列答案
相关题目
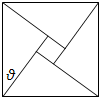（2012•仪陇县模拟）四个全等的直角三角形围成一个大正方形，中间空出的部分是一个小正方形，这样就组成了一个“赵爽弦图”（如图）．如果小正方形面积为4，大正方形面积为74，直角三角形中较小的锐角为θ，那么tanθ的值是（ ）