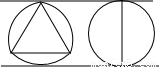
题目内容
如图，以边长为a的等边三角形各顶点为圆心，以a为半径在对边之外作弧，所得的曲边三角形是一种被称作“常宽的”曲线．此曲线的周长与直径为a的圆的周长之比是（ ）
A．3：1
B．1：3
C．1：2
D．1：1
【答案】分析：先根据弧长公式求出这种常宽曲线的周长，再根据圆的周长公式求得直径为a的圆的周长，再求比值即可．
解答：解：∵三段弧的圆心角都等于60°，
∴曲线的周长=3×
=πa；
∵直径为a的圆的周长=πa；
∴曲线的周长与直径为a的圆的周长之比=1：1．
故选D．
点评：本题考查的是正多边形和圆，熟记等边三角形的性质及弧长公式是解答此题的关键．
解答：解：∵三段弧的圆心角都等于60°，
∴曲线的周长=3×
=πa；∵直径为a的圆的周长=πa；
∴曲线的周长与直径为a的圆的周长之比=1：1．
故选D．
点评：本题考查的是正多边形和圆，熟记等边三角形的性质及弧长公式是解答此题的关键．
练习册系列答案
相关题目
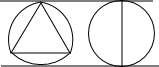如图，以边长为a的等边三角形各定点为圆心，以a为半径在对边之外作弧，由这三段圆弧组成的曲线是一种常宽曲线．此曲线的周长与直径为a的圆的周长之比是（ ）| A、1：1 | B、1：3 | C、3：1 | D、1：2 |
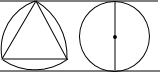（2011•江干区模拟）如图，以边长为a的等边三角形各顶点为圆心，以a为半径在对边之外作弧，所得的曲边三角形是一种被称作“常宽的”曲线．此曲线的周长与直径为a的圆的周长之比是（ ）
