题目内容
【题目】如图所示，点O为直线BD上的一点，OC⊥OA，垂足为点O，∠COD=2∠BOC，求∠AOB的度数．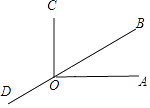
【答案】解：∵点O为直线BD上一点，
∴∠COD+∠B0C=180°，
将∠COD=2∠B0C代入，
得2∠BOC+∠BOC=180°，
解得∠BOC=60°，
∴∠AOB=∠COA﹣∠BOC=90°﹣60°=30°
【解析】先由点O为直线BD上一点，根据邻补角定义得出∠COD+∠BOC=180°，将∠COD=2∠B0C代入，求出∠BOC=60°，再根据∠AOB=∠COA-∠BOC即可求解.
【考点精析】通过灵活运用角的运算和垂线的性质，掌握角之间可以进行加减运算；一个角可以用其他角的和或差来表示；垂线的性质：1、过一点有且只有一条直线与己知直线垂直．2、垂线段最短即可以解答此题．
练习册系列答案
中考解读考点精练系列答案
相关题目
【题目】某校初三（1）班进行立定跳远训练，以下是李超和陈辉同学六次的训练成绩（单位：m）
1 | 2 | 3 | 4 | 5 | 6 | |
李超 | 2.50 | 2.42 | 2.52 | 2.56 | 2.48 | 2.58 |
陈辉 | 2.54 | 2.48 | 2.50 | 2.48 | 2.54 | 2.52 |
（1）李超和陈辉的平均成绩分别是多少？
（2）分别计算两人的六次成绩的方差，哪个人的成绩更稳定？为什么？
（3）若预知参加级的比赛能跳过2.55米就可能得冠军，应选哪个同学参加？为什么？
