题目内容
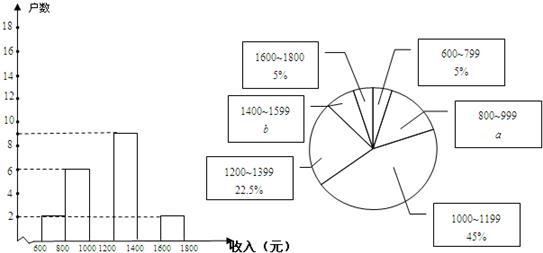
在今年“五•一”长假期间,某学校团委会要求学生参加一项社会调查活动.八年级学生小青想了解她所居住的小区500户居民的家庭收入情况,从中随机调查了40户居民家庭的收入情况(收入取整数,单位:元)并绘制了如下的频数分布表和频数分布直方图.| 分组 | 频数 | 频率 |
| 600~799 | 2 | 0.050 |
| 800~999 | 6 | 0.150 |
| 1000~1199 | 0.450 | |
| 1200~1399 | 9 | 0.225 |
| 1400~1599 | ||
| 1600~1800 | 2 | 0.050 |
| 合计 | 40 | 1.000 |
(1)补全频数分布表:
(2)补全频数分布直方图;
(3)这40户家庭收入的中位数落在哪一个小组;
(4)请你估计该居民小区家庭收入较低(不足1000元)的户数大约有多少户?
【答案】分析:(1)根据频率=频数÷总数,由表格中已知数据计算未知数据;
(2)根据(1)中的计算,根据各组之间的高的比,进行正确画图;
(3)根据中位数的概念,应是第20个和第21个平均数,然后根据各组的频数即可判断中位数落在哪一组;
(4)首先计算样本中该居民小区家庭收入较低(不足1000元)的户数所占的频率,然后计算500户居民中该居民小区家庭收入较低(不足1000元)的户数.
解答:解:(1)第三组的频数=40×0.45=18;第五组的频数=40-37=3,频率=3÷40=0.07;
(2)如图:
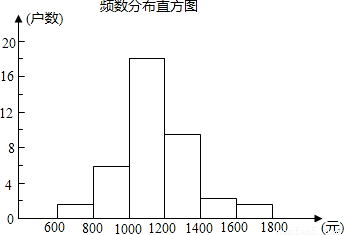
(3)第20个和第21个数都落在第三组,所以这40户家庭收入的中位数在1000~1199这个小组(或答第三小组);
(4)因为收入较低的频率为0.050+0.150=0.2,
所以该小区500户居民的家庭收入较低的户数为0.2×500=100户.
点评:掌握频率、频数、总数三者之间的关系:频率=频数÷总数;理解中位数的概念;能够根据样本估计总体.
(2)根据(1)中的计算,根据各组之间的高的比,进行正确画图;
(3)根据中位数的概念,应是第20个和第21个平均数,然后根据各组的频数即可判断中位数落在哪一组;
(4)首先计算样本中该居民小区家庭收入较低(不足1000元)的户数所占的频率,然后计算500户居民中该居民小区家庭收入较低(不足1000元)的户数.
解答:解:(1)第三组的频数=40×0.45=18;第五组的频数=40-37=3,频率=3÷40=0.07;
(2)如图:
| 分组 | 频数 | 频率 |
| 600~799 | 2 | 0.050 |
| 800~999 | 6 | 0.150 |
| 1000~1199 | 18 | 0.450 |
| 1200~1399 | 9 | 0.225 |
| 1400~1599 | 3 | 0.07 |
| 1600~1800 | 2 | 0.050 |
| 合计 | 40 | 1.000 |

(3)第20个和第21个数都落在第三组,所以这40户家庭收入的中位数在1000~1199这个小组(或答第三小组);
(4)因为收入较低的频率为0.050+0.150=0.2,
所以该小区500户居民的家庭收入较低的户数为0.2×500=100户.
点评:掌握频率、频数、总数三者之间的关系:频率=频数÷总数;理解中位数的概念;能够根据样本估计总体.

练习册系列答案
相关题目
在今年“五•一”长假期间,某学校团委会要求学生参加一项社会调查活动.八年级学生小青想了解她所居住的小区500户居民的家庭收入情况,从中随机调查了40户居民家庭的收入情况(收入取整数,单位:元)并绘制了如下的频数分布表和频数分布直方图.
根据以上提供的信息,解答下列问题:
(1)补全频数分布表:
(2)补全频数分布直方图;
(3)这40户家庭收入的中位数落在哪一个小组;
(4)请你估计该居民小区家庭收入较低(不足1000元)的户数大约有多少户?
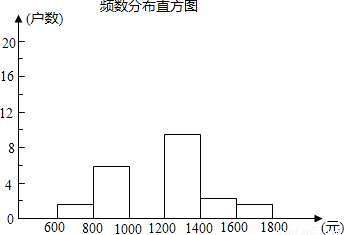
| 分组 | 频数 | 频率 |
| 600~799 | 2 | 0.050 |
| 800~999 | 6 | 0.150 |
| 1000~1199 | 0.450 | |
| 1200~1399 | 9 | 0.225 |
| 1400~1599 | ||
| 1600~1800 | 2 | 0.050 |
| 合计 | 40 | 1.000 |
(1)补全频数分布表:
(2)补全频数分布直方图;
(3)这40户家庭收入的中位数落在哪一个小组;
(4)请你估计该居民小区家庭收入较低(不足1000元)的户数大约有多少户?

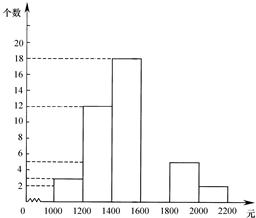 5、某中学为了培养学生的社会实践能力,今年“五•一”长假期间要求学生参加一项社会调查活动.为此,小明在他所居住小区的600个家庭中,随机调查了50个家庭在新工资制度实施后的收入情况,并绘制了如下的频数分布表和频数分布直方图.(收入取整数,单位:元)
5、某中学为了培养学生的社会实践能力,今年“五•一”长假期间要求学生参加一项社会调查活动.为此,小明在他所居住小区的600个家庭中,随机调查了50个家庭在新工资制度实施后的收入情况,并绘制了如下的频数分布表和频数分布直方图.(收入取整数,单位:元)
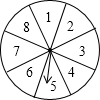 的机会(如图),如果规定当圆盘停下来时,指针指向8就中一等奖,指向2或5就中二等奖,指向其余数字不中奖.
的机会(如图),如果规定当圆盘停下来时,指针指向8就中一等奖,指向2或5就中二等奖,指向其余数字不中奖.