题目内容
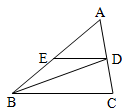
【题目】如图,已知△ABC中,BD是∠ABC的角平分线,DE∥BC,交AB于E,∠A=60°,∠C=80°,求:△BDE各内角的度数.
【答案】∠ABD=20°;∠BDE=20°;∠BED=140°.
【解析】
试题分析:根据∠A和∠C的度数求出∠ABC的度数,根据BD为角平分线得出∠ABD和∠CBD的度数,根据平行得出∠EDB的度数,最后根据△BDE的内角和求出∠BED的度数.
试题解析:因为∠A=60°,∠C=80°, 所以∠ABC=180°-∠A-∠C= 40°.
因为BD是∠ABC的角平分线, 所以∠ABD=∠CBD=20°.
又因为DE∥BC, 所以∠BDE=∠CBD=20°. 所以∠BED=180°-∠EBD-∠BDE=140°.

练习册系列答案
相关题目
【题目】小林在某商店购买商品A、B共三次,只有一次购买时,商品A、B同时打折(折扣相同),其余两次均按标价购买.三次购买商品A、B的数量和费用如下表:
购买商品A的数量/个 | 购买商品B的数量/个 | 购买总费用/元 | |
第一次购物 | 6 | 5 | 1140 |
第二次购物 | 3 | 7 | 1110 |
第三次购物 | 9 | 8 | 1062 |
(1)小林以折扣价购买商品A、B是第 次购物;
(2)求出商品A、B的标价;
(3)若商品A、B的折扣相同,问商店是打几折出售这两种商品的?