题目内容
如图，使△ABC≌△ADC成立的条件是
- A.AB=AD，∠B=∠D
- B.AB=AD，∠ACB=∠ACD
- C.BC=DC，∠BAC=∠DAC
- D.AB=AD，∠BAC=∠DAC
D
分析：本题重点考查三角形全等判定定理SAS，强调的对应角是已知两条对应边的夹角．
解答：∵AB=AD，∠BAC=∠DAC，
又AC=AC，
∴△ABC≌△ADC （SAS），
∴D是可以使△ABC≌△ADC成立的，
SSA不能判断全等．所以A、B、C都不能选．
故选D
点评：本题考查了全等三角形的判定；普通两个三角形全等共有四个定理，即AAS、ASA、SAS、SSS，直角三角形可用HL定理，但AAA、SSA，无法证明三角形全等，本题是一道较为简单的题目．
分析：本题重点考查三角形全等判定定理SAS，强调的对应角是已知两条对应边的夹角．
解答：∵AB=AD，∠BAC=∠DAC，
又AC=AC，
∴△ABC≌△ADC （SAS），
∴D是可以使△ABC≌△ADC成立的，
SSA不能判断全等．所以A、B、C都不能选．
故选D
点评：本题考查了全等三角形的判定；普通两个三角形全等共有四个定理，即AAS、ASA、SAS、SSS，直角三角形可用HL定理，但AAA、SSA，无法证明三角形全等，本题是一道较为简单的题目．
练习册系列答案
阅读快车系列答案
相关题目
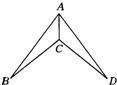38、如图，使△ABC≌△ADC成立的条件是（ ）
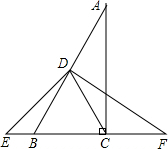已知：如图，在△ABC中，∠ACB=90°点D是AB的中点，延长BC到点F，延长CB到点E，使CF=BE，连接DE、DC、DF．
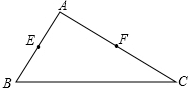如图，Rt△ABC中，∠BAC=90°，AB=6，AC=8，且E、F分别是两直角边AB、AC上的中点．
