题目内容
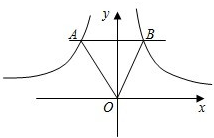 如图是双曲线y=
如图是双曲线y=| 2 |
| x |
| 3 |
| x |
| 5 |
| 2 |
| 5 |
| 2 |
分析:根据反比例函数的比例系数的几何意义即可求得S△AOC和S△ABO,则△AOB的面积可以求得.
解答: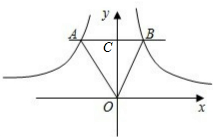 解:S△AOC=
解:S△AOC=
×3=
,
S△OBC=
×2=1,
∴S△ABO=S△AOC+S△OBC=
+1=
.
故答案是:
.
 解:S△AOC=
解:S△AOC=| 1 |
| 2 |
| 3 |
| 2 |
S△OBC=
| 1 |
| 2 |
∴S△ABO=S△AOC+S△OBC=
| 3 |
| 2 |
| 5 |
| 2 |
故答案是:
| 5 |
| 2 |
点评:以比例系数k的几何意义为知识基础,结合正方形的面积设计了一道中考题,由此也可以看出比例系数k的几何意义在解答问题中的重要性.

练习册系列答案
相关题目
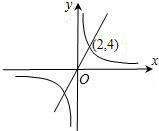 如图,直线y=2x与双曲线y=
如图,直线y=2x与双曲线y=| k |
| x |
| A、(-2,-4) |
| B、(-2,4) |
| C、(-4,-2) |
| D、(2,-4) |
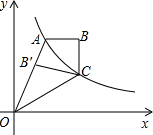 如图,双曲线
如图,双曲线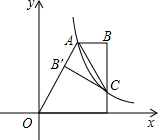 如图,双曲线
如图,双曲线 如图,点M是双曲线y=
如图,点M是双曲线y=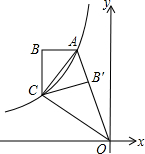 如图,双曲线
如图,双曲线