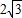题目内容
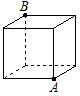
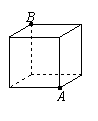
 如图,是一个棱长为2的正方体,一只蜘蛛在顶点A处,一只小昆虫在顶点B处,则蜘蛛接近小昆虫时所爬行的最短路线的长是
如图,是一个棱长为2的正方体,一只蜘蛛在顶点A处,一只小昆虫在顶点B处,则蜘蛛接近小昆虫时所爬行的最短路线的长是
- A.6
- B.2+
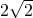
- C.

- D.
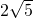
D
分析:把此正方体的一面展开,然后在平面内,利用勾股定理求点A和B点间的线段长,即可得到蜘蛛爬行的最短距离.
解答:在直角三角形中,一条直角边长等于棱长,另一条直角边长等于两条棱长之和,
利用勾股定理可求得AB=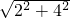 =2
=2 .
.
故选D.
点评:本题考查了勾股定理的拓展应用.“化曲面为平面”是解决“怎样爬行最近”这类问题的关键.
分析:把此正方体的一面展开,然后在平面内,利用勾股定理求点A和B点间的线段长,即可得到蜘蛛爬行的最短距离.
解答:在直角三角形中,一条直角边长等于棱长,另一条直角边长等于两条棱长之和,
利用勾股定理可求得AB=
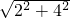 =2
=2 .
.故选D.
点评:本题考查了勾股定理的拓展应用.“化曲面为平面”是解决“怎样爬行最近”这类问题的关键.

练习册系列答案
 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目
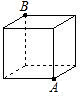 如图,是一个棱长为2的正方体,一只蜘蛛在顶点A处,一只小昆虫在顶点B处,则蜘蛛接近小昆虫时所爬行的最短路线的长是( )
如图,是一个棱长为2的正方体,一只蜘蛛在顶点A处,一只小昆虫在顶点B处,则蜘蛛接近小昆虫时所爬行的最短路线的长是( )| A、6 | ||
B、2+2
| ||
C、2
| ||
D、2
|