题目内容
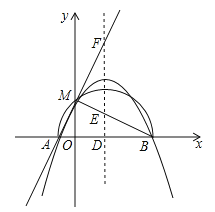
【题目】如图,直线![]() 与
与![]() 轴、
轴、![]() 轴分别相交于点
轴分别相交于点![]() 和点
和点![]() .
.
(1)直接写出坐标:点![]() ,点
,点![]() .
.
(2)以线段![]() 为一边在第一象限内作正方形
为一边在第一象限内作正方形![]() .
.
则:①顶点![]() 的坐标是 ,
的坐标是 ,
②若点![]() 在双曲线
在双曲线![]() 上,试探索:将正方形
上,试探索:将正方形![]() 沿
沿![]() 轴向左平移多少个单位长度时,点
轴向左平移多少个单位长度时,点![]() 恰好落在该双曲线上.
恰好落在该双曲线上.
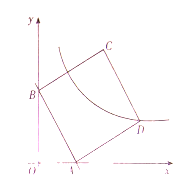
【答案】(1)![]() ;(2)①
;(2)①![]() ;②将正方形
;②将正方形![]() 沿
沿![]() 轴向左平移1个单位长度时,点
轴向左平移1个单位长度时,点![]() 恰好落在该双曲线上
恰好落在该双曲线上
【解析】
(1)利用一次函数图象上点的坐标特征可求出点A,B的坐标;
(2)①过点D作DE⊥x轴于点E,易证△OAB≌△EDA,利用全等三角形的性质可求出点D的坐标;
②由点D的坐标,利用待定系数法可求出双曲线的解析式,过点C作CF⊥y轴于点F,易证△CFB≌△AOB,利用全等三角形的性质可求出点C的坐标,再利用反比例函数图象上点的坐标特征可得出当点C落在双曲线上时正方形ABCD沿x轴向左平移的距离.
当x=0时,y=-2x+2=2,
∴点B的坐标为(0,2);
当y=0时,-2x+2=0,
解得:x=1,
∴点A的坐标为(1,0).
故答案为:(1,0);(0,2).
(2)①过点D作DE⊥x轴于点E,如图1所示.
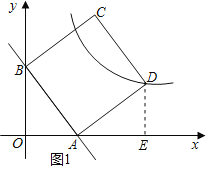
∵∠OBA+∠OAB=90°,∠OAB+∠EAD=90°,
∴∠OBA=∠EAD.
在△OAB和△EDA中,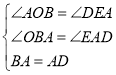 ,
,
∴△OAB≌△EDA(AAS),
∴AE=BO=2,DE=AO=1,
∴点D的坐标为(3,1).
②将点D(3,1)代入y=![]() ,得:1=
,得:1=![]() ,
,
∴k=3,
∴y=![]()
过点C作CF⊥y轴于点F,如图2所示.
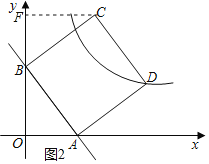
同(1)可证出△CFB≌△AOB,
∴BF=AO=1,CF=BO=2,
∴点C的坐标为(2,3).
当y=3时,![]() =3,
=3,
解得:x=1,
∵2-1=1,
∴将正方形ABCD沿x轴向左平移1个单位长度时,点C恰好落在该双曲线上.

 名校课堂系列答案
名校课堂系列答案【题目】经过一年多的精准帮扶,小明家的网络商店(简称网店)将红枣、小米等优质土特产迅速销往全国,小明家网店中红枣和小米这两种商品的相关信息如下表:
商品 | 红枣 | 小米 |
规格 | 1kg/袋 | 2kg/袋 |
成本(元/袋) | 40 | 38 |
售价(元/袋) | 60 | 54 |
根据上表提供的信息,解答下列问题:
(1)已知今年前五个月,小明家网店销售上表中规格的红枣和小米共3000kg,获得利润4.2万元,求这前五个月小明家网店销售这种规格的红枣多少袋;
(2)根据之前的销售情况,估计今年6月到10月这后五个月,小明家网店还能销售上表中规格的红枣和小米共2000kg,其中,这种规格的红枣的销售量不低于600kg.假设这后五个月,销售这种规格的红枣味x(kg),销售这种规格的红枣和小米获得的总利润为y(元),求出y与x之间的函数关系式,并求出这后五个月,小明家网店销售这种规格的红枣和小米至少获得总利润多少元.