题目内容
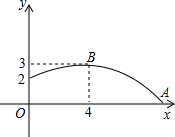 如图,是一学生掷铅球时,铅球行进高度y(cm)的函数图象,点B为抛物线的最高点,则该同学的投掷成绩为________米.
如图,是一学生掷铅球时,铅球行进高度y(cm)的函数图象,点B为抛物线的最高点,则该同学的投掷成绩为________米.
(4+4 )
)
分析:根据函数的顶点B的坐标设解析式为y=a(x-4)2+3,把(0,2)代入得出2=a(0-4)2+3,求出a,得出函数的解析式是y=- (x-4)2+3,把y=0代入解析式,求出方程的解即可.
(x-4)2+3,把y=0代入解析式,求出方程的解即可.
解答:∵函数的图象的最高点是B,B的坐标是(4,3),
∴设函数的解析式是y=a(x-4)2+3,
∵图象过(0,2)点,
∴代入得:2=a(0-4)2+3,
解得:a=- ,
,
∴函数的解析式是y=- (x-4)2+3,
(x-4)2+3,
把y=0代入解析式得:0=-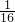 (x-4)2+3,
(x-4)2+3,
解得:x1=4+4 ,x2=4-4
,x2=4-4 ,
,
∴A(4+4 ,0),
,0),
故答案为:(4+4 ).
).
点评:本题考查了二次函数的应用,关键是求出二次函数的解析式,用了数形结合思想和转化思想.
 )
)分析:根据函数的顶点B的坐标设解析式为y=a(x-4)2+3,把(0,2)代入得出2=a(0-4)2+3,求出a,得出函数的解析式是y=-
 (x-4)2+3,把y=0代入解析式,求出方程的解即可.
(x-4)2+3,把y=0代入解析式,求出方程的解即可.解答:∵函数的图象的最高点是B,B的坐标是(4,3),
∴设函数的解析式是y=a(x-4)2+3,
∵图象过(0,2)点,
∴代入得:2=a(0-4)2+3,
解得:a=-
 ,
,∴函数的解析式是y=-
 (x-4)2+3,
(x-4)2+3,把y=0代入解析式得:0=-
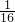 (x-4)2+3,
(x-4)2+3,解得:x1=4+4
 ,x2=4-4
,x2=4-4 ,
,∴A(4+4
 ,0),
,0),故答案为:(4+4
 ).
).点评:本题考查了二次函数的应用,关键是求出二次函数的解析式,用了数形结合思想和转化思想.

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目
 如图,是一学生掷铅球时,铅球行进高度y(cm)的函数图象,点B为抛物线的最高点,则该同学的投掷成绩为
如图,是一学生掷铅球时,铅球行进高度y(cm)的函数图象,点B为抛物线的最高点,则该同学的投掷成绩为