题目内容
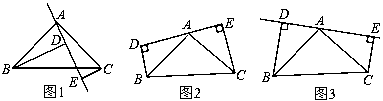
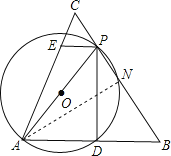
【题目】已知,如图,a,b,c分别是ΔABC中∠A,∠B,∠C的对边,P为BC上一点,以AP为直径的圆O交AB于D,PE∥AB交AC于E,b,c是方程x2+kx+9=0的两根,且(b2+c2)(b2+c2-14)-72=0,锐角B的正弦值等于![]() 。
。
(1)求K的值;
(2)设BD=x,求四边形ADPE的面积为S关于x的函数关系式;
(3)问圆O是否能与BC相切?若能请求出x的值;若不能,请说明理由。

【答案】(1)k=-6 (2)![]() (3)能,
(3)能, ![]() .
.
【解析】试题分析:(1)求出b2+c2=18,根据根与系数的关系求出b+c=-k,bc=9,代入得出方程(-k)2-2×9=18,求出即可;
(2)求出方程的解,得出AB=AC=3,根据sinB=![]() =
=![]() ,设PD=2
,设PD=2![]() y,PD=3y,在Rt△BDP中,由勾股定理求出y=x,得出PD=2
y,PD=3y,在Rt△BDP中,由勾股定理求出y=x,得出PD=2![]() x,PB=3x,求出BC,根据△CPE∽△CBA,得出比例式求出PE,代入S=
x,PB=3x,求出BC,根据△CPE∽△CBA,得出比例式求出PE,代入S=![]() (PE+AD)×PD求出即可;(3)根据圆的切线的性质,当∠APB=90°时,圆O能与BC相切,根据等腰三角形性质得出BD=DC=
(PE+AD)×PD求出即可;(3)根据圆的切线的性质,当∠APB=90°时,圆O能与BC相切,根据等腰三角形性质得出BD=DC=![]() ,根据PB=3x=
,根据PB=3x=![]() 求出即可.
求出即可.
试题解析:(1)∵(b2+c2)(b2+c214)72=0,
∴(b2+c2)214(b2+c2)72=0,
解得:b2+c2=18,b2+c2=4(舍去),
∵b,c是方程x2+kx+9=0的两根,
∴b+c=k,bc=9,
∴b2+c2=(b+c)22bc=18,
即(k)22×9=18,
解得:k=6,k=6,
∵b+c=k,c、b是三角形的边长,
∴k=6舍去,
即k=6;
(2)把k=6代入方程得:x26x+9=0,
解得:x1=x2=3,
即b=c=3,
AB=AC=3,
∵AP是直径,
∴∠ADP=90=∠BDP,
∵sinB=![]() ,
,
∴![]() =
=![]() ,
,
设PD=![]() y,BD=3y,在Rt△BDP中,由勾股定理得:PD2+BD2=PB2,
y,BD=3y,在Rt△BDP中,由勾股定理得:PD2+BD2=PB2,
即(![]() y)2+x2=(3y)2,
y)2+x2=(3y)2,
解得:y=x,
PD=![]() x,PB=3x,
x,PB=3x,
过A作AN⊥BC于N,
∵AB=3,sinB=![]() ,
,
∴AN=![]() ,
,
由勾股定理得:BN=1,
∵AB=AC,AN⊥BC,
∴CN=BN=1,
BC=2,
∵PE∥AB,
∴△CPE∽△CBA,
∴![]() ,
,
∴![]() ,
,
∴PE=![]() x+3,
x+3,
∴四边形ADPE的面积S=![]() (PE+AD)×PD=
(PE+AD)×PD=![]() ×(
×(![]() x+3+3x)×
x+3+3x)×![]() x=
x=![]() x2+
x2+![]() x,
x,
答:四边形ADPE的面积为S关于x的函数关系式是S=![]() x2+
x2+![]() x.
x.
(3)圆O能与BC相切,
理由是:根据圆的切线的性质,当∠APB=90时,圆O能与BC相切,
∵AP是直径,
∴∠ADP=90,
∵AC=AB=3,BC=2,
∴BD=DC=1,
由(2)知:PB=3x=1,
x=![]() ,
,
答:圆O能与BC相切,x的值是![]() .
.

 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案